この記事は Stan Advent Calendar 2016 の12月8日のエントリーです。Advent Calendarはこれまで見るものであって自分で参加するものとは思っておらず,ノリで手を挙げてしまったので,いろいろと不安ではありますがやってみます。間違っているところ,もっとこうしたほうが良いなどがありましたら教えていただけると喜びます。
概要としては,以下のようなものになっています。
- 一般化極値分布について
- 高松市の最大降水量を一般化極値分布使って推定してみた
- 高松市の最大降水量は増加しているか推定してみた
一般化極値分布について
共同研究の関連で,最大値を分析する必要出てきまして,一般化極値分布という分布を使うことになりました。一般化極値分布は,最大値や最小値に適用できる分布のようです。
今回,共同研究で取っているデータは自分でいつでもとれるというものではありませんが,心理学の中でも反応時間などを従属変数とする実験の場合,もしかすると最大値や最小値を分析するとおもしろいことがわかるかもしれません。データの安定性を捨て去ってしまっている気がするので,あくまで「かも」です。個人的には最大値を使おうと思うと,反応時間は,ふつうに正規分布を使ってしまうか,ちゃんとexガウシアン分布を使っていつも通りの分析をした後に,補足的に最大値についても扱ってやるのがよいかなと思ったりしています。
一般化極値分布とは,極値分布に一般性をもたせた分布のことをいうようです。
以下にWikipediaから極値分布の説明を引用します。
確率論および統計学において、極値分布(きょくちぶんぷ)とは、ある分布関数にしたがって生じた大きさ n の標本 X1,X2, …, Xn のうち、x 以上 (あるいは以下) となるものの個数がどのように分布するかを表す、連続型の確率分布モデルである。特に最大値や最小値などが漸近的に従う分布であり、河川の氾濫、最大風速、最大降雨量、金融におけるリスク等の分布に適用される。Wikipediaより
MATLABのページで一般化極値分布の説明のようなものと分布の形も見られました(リンク)。MATLABのページの説明も以下に引用します。
一般化極値 (GEV) 分布は、1 種、2 種、および 3 種の極値分布を 1 つのファミリにまとめるので、可能な形状を連続的にとることができます。一般化極値分布は、位置パラメーター mu、スケール パラメーター sigma および形状パラメーター k でパラメーター化されています。k < 0 の場合、GEV は 3 種の極値と同等です。k > 0 の場合、GEV は 2 種の極値と同等です。k が 0 に近い極限では、GEV は 1 種の極値に近づきます。
分布の形を見てみると,なるほど,確かに正規分布とは違うようです。3つパラメタがあり,X軸の全体的な動きは位置パラメタのmu,分散のような分布のふくらみはスケールパラメタのsigma,歪度のような分布のゆがみは形状パラメタのkで表すみたいです。以下では,形状パラメタはkではなくxiで表現しています。細かいことはよくわかっていませんが,今回はこの一般化極値分布をつかった推定を,rstanパッケージ(version 2.12)を用いて行ってみたいと思っています。
残念なことに一般化極値分布はまだstanには実装されていません。ということで,一般化極値分布をstanで使えるようにしたいと思います。とはいっても,私にはよくわからないことも多いので,Google先生に頼りました。すると極値分布をstanで使うには,といった議論がgoogleグループでなされていました(リンク)。この中で,極値分布の実装についてのコードが紹介されていたため,今回はこのページのコードをお借りして,少し改変して使用しています。なお,BUGSには一般化極値分布が実装されています(OpenBUGSのマニュアル)。
rstanではfunctionブロックで一般化極値分布を定義してあげるわけですが,こんな感じです。
functions {
real gev_lpdf (real y, real mu, real sigma, real xi){
real z;
z = 1 + (y - mu) * xi/sigma;
return -log(sigma) - (1 + 1/xi)*log(z) - pow(z,-1/xi);
}
}
高松市の最大降水量を一般化極値分布使って推定してみた
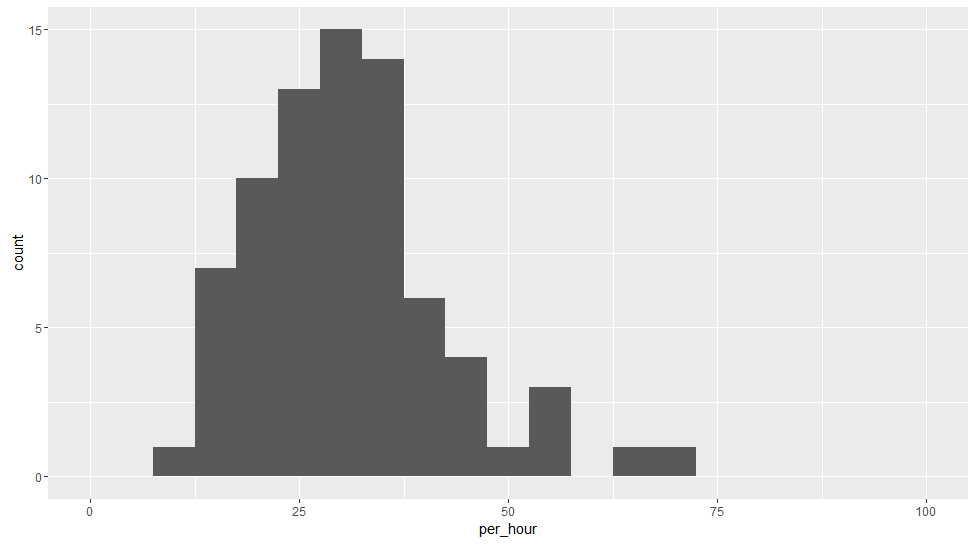
今回は,気象庁で公開している降水量データに一般化極値分布をあてはめてみたいと思います。使用するデータは,香川県高松市の1941年から2016年まで76年間の各年における1時間あたりの最大降水量です。
これをヒストグラムにするとこんな感じです。うん,歪んでいるのがわかりますね。正規分布ではなさそうです。
使用したstanコードはこんな感じです。
functions {
real gev_lpdf (real y, real mu, real sigma, real xi){
real z;
z = 1 + (y - mu) * xi/sigma;
return -log(sigma) - (1 + 1/xi)*log(z) - pow(z,-1/xi);
}
}
data {
int<lower=0> N;
real Y[N];
}
parameters {
real <lower = -0.5, upper = 0.5> xi;
real <lower = 0, upper = 10> sigma;
real <lower = 0, upper = 100> mu;
}
model {
sigma ~ uniform(0, 10);
mu ~ uniform(0, 100);
xi ~ uniform(-.5, .5);
for(i in 1:N) {
Y[i] ~ gev(mu, sigma, xi);
}
}
generated quantities {
real p;
real predict;
p = uniform_rng (0, 1);
predict = (xi != 0) ? (mu - (sigma/xi) *(1-(-log (1 -p))^ -xi))
: (mu - sigma*-log(1 -p));
over_50 = (predict > 50) ? 1 : 0;
}
- 14~17行目:parameterブロックで,一般化極値分布の各パラメタの範囲を指定しています。
- 20~23行目:modelブロックでmu, sigma,xiそれぞれの事前分布を設定しています。xiの値の範囲を広くしすぎると推定がちょっと変なことになることがあるみたいです。
- 30~35行目:事後予測分布も作りたいのですが,functionブロックで定義した分布には_rng()による乱数発生はできないようです。そのため,generated quantitiesブロックで推定したパラメタを元に一般化局地分布の事後予測分布を発生させるようにしています(数式の参考ページ)。xi = 0というケースは稀かもしれませんが,xiの値によって,適用する式が変わるので,分岐を作っています。ちなみに,rstan2.12ではif_else()よりも”:?”というC++の記法が推奨されているようです。warningメッセージは出ますが,if_else()でもちゃんと走ります。
- 36行目:一般化極値分布は,最大値や最小値がある値を超えるリスクがどのくらいか算出するのに役立つようなので,最大降水量が50mmを超える確率を算出させています
rstanの出力はこんな感じ。
Inference for Stan model: gev_stan02_01.
2 chains, each with iter=30000; warmup=5000; thin=1;
post-warmup draws per chain=25000, total post-warmup draws=50000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
xi 0.01 0.00 0.08 -0.12 -0.04 0.01 0.06 0.19 19850 1
sigma 8.94 0.00 0.62 7.65 8.51 8.98 9.43 9.92 20262 1
mu 25.67 0.01 1.07 23.56 24.95 25.67 26.38 27.79 21667 1
p 0.50 0.00 0.29 0.03 0.25 0.50 0.75 0.97 50000 1
predict 31.04 0.05 12.06 13.97 22.79 29.04 36.94 59.51 49721 1
over_50 0.07 0.00 0.25 0.00 0.00 0.00 0.00 1.00 49832 1
lp__ -285.89 0.01 1.33 -289.30 -286.51 -285.55 -284.91 -284.36 13075 1
- 10行目:事後予測分布の予測値の中央値は28.90
- 11行目:1時間の降水量が50mmを超える確率は7%
- バーンイン区間を除くと50000回のサンプリングをしているのに,n_effが小さいような気がします。
やっぱり香川ってそんなに雨ふらないんだな(小並感)
事後予測分布を描くとこんな感じです。元データと似ている気がします。
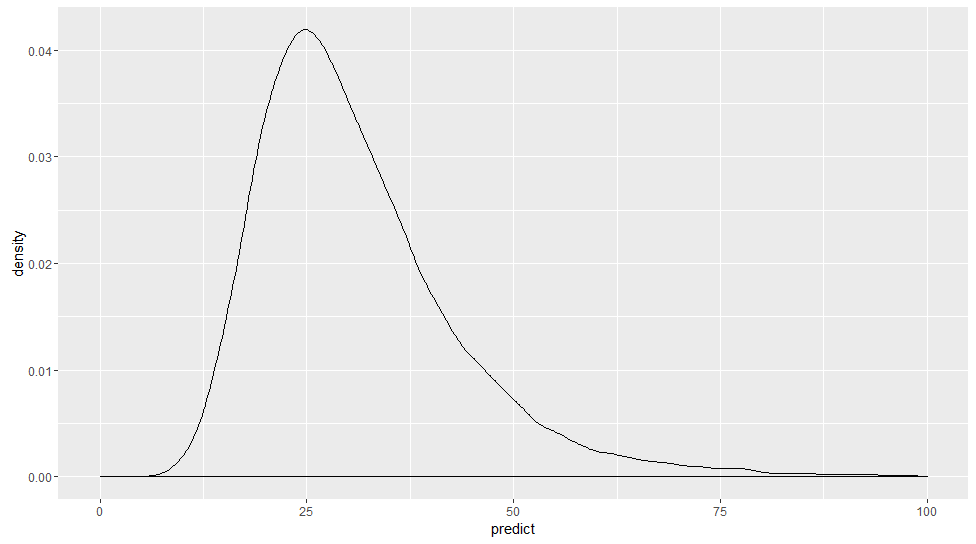
分位点を並べて比べてみます。
> print(q1, digits = 4) # 元データの分位点 5% 10% 20% 30% 40% 50% 60% 70% 80% 90% 95% 15.82 17.75 20.40 24.85 27.50 29.50 32.50 34.50 38.00 44.40 52.78 > print(q2, digits = 4) # 一般化極値分布の事後予測分布の分位点 5% 10% 20% 30% 40% 50% 60% 70% 80% 90% 95% 15.98 18.26 21.28 23.79 26.16 28.68 31.54 34.94 39.47 47.09 54.63
値が大きくなってくるとちょっとずれているような気もしますが,やっぱり,いい感じに推定できている気がします。
これ実は,googleで紹介されていたparameterブロックのstanコードは
parameters {
real <lower = -0.5, upper = 0.5> xi;
real <lower = 0, upper = 10> sigma;
real<lower = if_else( xi < 0, sigma/xi, negative_infinity() ),
upper = if_else( xi > 0, positive_infinity(), Y[N] + sigma/xi )> mu;
}
だったのですが,このコードを使ってMCMCするとn_effの数が半分以下になってしまい,どうにも収束しにくくなるみたいです。本来はxiの値によってmuの範囲が変化するのですが,今回はmuの範囲は単純なものにしても推定値が変わらないこともあったので,MCMCの収束を優先しました。ちなみに,別データで試した時には,real
本当なら正規分布での推定とWAIC使って比較までしたほうがよいのかもしれませんが…ゴニョゴニョ
高松市の最大降水量は増加しているか推定してみた
異常気象が増えているとか聞くことがあります。もう何年も前かもですがゲリラ豪雨とかいう言葉もできましたし。最大降水量って昔と比べて増えているのかを検討してみたいと思います。本来はstan advent calender 12月1日のkosugitti先生のように状態空間モデルを使うべきかとも思ったのですが,状態空間モデルを適用するには
- 各年の1時間あたりの最大降水量だと観測が正確には一定間隔とはいえない
- 観測点も不足していそう
- まだ自分が理解できていない(超重要)
ということで,単純に直線をあてはまる西暦を説明変数とする一般化極値回帰を行うことにしました。これにもいろいろと問題があるとは思いますので,お気づきの方は教えてください。
stanコードはこんな感じです。一般化極値分布のx軸方向への動きを示す平均値的なmu_baseに対して西暦の影響があるかを検討しようとしています。
functions {
real gev_lpdf (real y, real mu, real sigma, real xi){
real z;
z = 1 + (y - mu) * xi/sigma;
return -log(sigma) - (1 + 1/xi)*log(z) - pow(z,-1/xi);
}
}
data {
int<lower=0> N;
real Y[N];
int X[N];
}
parameters {
real <lower = -0.5, upper = 0.5> xi;
real <lower = 0, upper = 10> sigma;
real a;
real b;
}
transformed parameters {
real mu_base[N];
for (i in 1:N)
mu_base[i] = a + b*X[i];
}
model {
sigma ~ uniform(0, 10);
xi ~ uniform(-.5, .5);
for(i in 1:N) {
Y[i] ~ gev(mu_base[i], sigma, xi);
}
}
generated quantities {
real over_0;
over_0 = step (b);//(b > 0) ? 1:0;
}
- 19, 20行目:平均値のmu_baseを予測する切片aと回帰係数bを定義しています。
- 39, 40行目:回帰係数bが0以上である確率を算出しています。
generated quantitiesブロックで,さっきと同じように事後予測分布まで作ろう思ったのですが,うまくコードが書けずに今回は断念しています。また,西暦の影響bが0以上である確率算出するため,over_0 = step (b)を加えています。
stanに読み込ませるデータセット作成とサンプリングは以下のような条件で行っています。これまでと同じです。
N <- length (dat01$per_hour)
data02 <- list (Y = dat01$per_hour, X = (dat01$year-1941), N = N)
model03 <- stan_model ("gev_stan03.stan")
fit04 <- sampling (model03,
data = data02,
init = myinits, # 初期値指定
chains = 2, # chainの数
iter = 30000, # 反復回数
warmup = 5000) # バーンイン区間
以下,推定結果です。
Inference for Stan model: gev_stan03.
2 chains, each with iter=30000; warmup=5000; thin=1;
post-warmup draws per chain=25000, total post-warmup draws=50000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
xi 0.02 0.00 0.08 -0.12 -0.03 0.02 0.07 0.20 18709 1
sigma 8.88 0.00 0.63 7.58 8.43 8.91 9.37 9.92 19395 1
a 23.60 0.02 1.93 19.80 22.32 23.60 24.89 27.36 15941 1
b 0.06 0.00 0.04 -0.03 0.03 0.06 0.08 0.14 17020 1
mu_base[1] 23.60 0.02 1.93 19.80 22.32 23.60 24.89 27.36 15941 1
mu_base[2] 23.66 0.01 1.89 19.91 22.40 23.66 24.92 27.35 16002 1
mu_base[3] 23.71 0.01 1.86 20.04 22.47 23.71 24.96 27.34 16068 1
・
・
・
mu_base[74] 27.62 0.01 1.82 23.99 26.41 27.63 28.85 31.14 30990 1
mu_base[75] 27.68 0.01 1.85 23.97 26.44 27.68 28.93 31.26 30507 1
mu_base[76] 27.73 0.01 1.89 23.96 26.47 27.74 29.01 31.39 30050 1
over_0 0.91 0.00 0.29 0.00 1.00 1.00 1.00 1.00 22286 1
lp__ -288.46 0.01 1.50 -292.22 -289.20 -288.12 -287.35 -286.58 13903 1
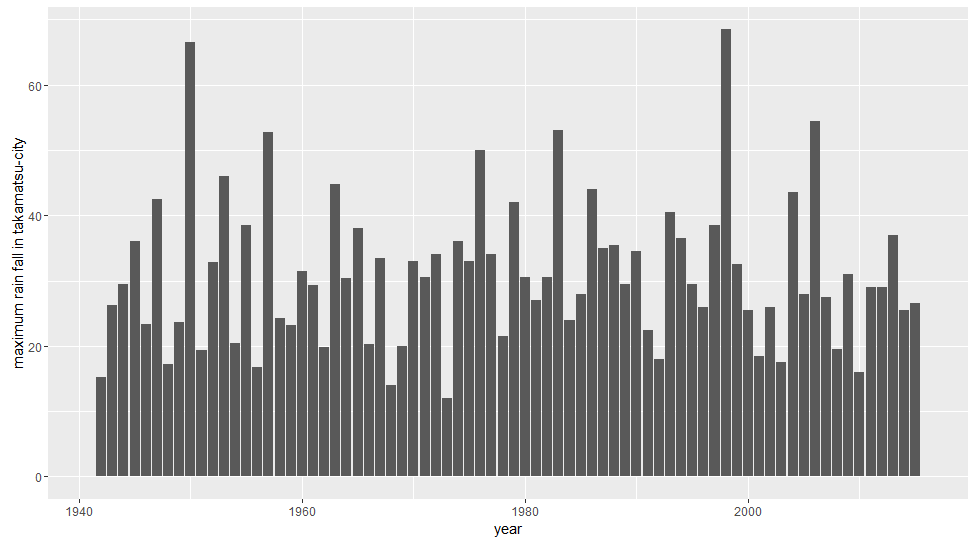
- 9行目:回帰係数bは0.06, 95%確信区間[-0.03, 0.06]なので効果がちゃんとあるとは言いにくい
- 19行目:回帰係数bが0を超える確率は91%,微妙なところです
高松市の1時間あたりの最大降水量はほとんど変化していないことがわかります。でもなんかちょっと増加しているような傾向もみられそうです。
全部思い通りにできたわけではありませんが,このような感じで実装されていない分布でもstanではユーザー側で実装させ,いろいろと遊ぶことができるので便利ですね。楽しいですね。
Pingback: 一般化極値分布の実装と状態空間モデルによる高松市の最大降水量の推移 – masaR web