情報仮説に基づく仮説の複雑性を算出する関数を作ってみました。ここではとりあえずコードだけですが公開しておきます。
詳しくは11月28日に開催される第3回 R勉強会@比治山大(広島) #HijiyamaRの発表でふれていきます(https://atnd.org/events/68737)。情報仮説のことについては,あとで記事にしようと思います。
complexH <- function(v_num, ie_num, e_num = 0){
# v_num: number of variables in hypotheses
# ie_num: number of inequality in hypotheses
# e_num: number of inequality in hypotheses
equality <- 10^e_num
# according Hoijtink et al. (2010), "="constrain is 10%
if ((v_num - e_num == 1) && (ie_num == 0)) {
list ("unconstraint" = 1,
# complexity of unconstrain hypotheses e.g., H0: m1, m2, ..., mn
"null" = 1/equality
# all "=" constrains e.g., H2: m1 = m2 = ... = mn
)
} else if (v_num <= ie_num) {
print ("error: chenge v_num > ie_num")
} else if (v_num <= e_num) {
print ("error: chenge v_num > e_num")
} else if ((v_num - e_num > 1) && (ie_num > 0)) {
list ("unconstraint" = 1/prod((v_num - ie_num + 1):v_num),
# only ">" constrains
"null" = 1/(prod((v_num - ie_num + 1):v_num) * equality)
# "=" and ">" constrains
)
} else {
print ("error: chenge v_num > (ie_num + e_num)")
}
}
基本的には,v_numには仮説に含まれる変数の数を,ie_numには仮説に含まれる不等号の数を,e_numには仮説に含まれる等号の数を入力すれば,仮説の複雑性を評価します。以下の使用例の場合,3つの変数があって,不等号は1つ,等号は1つというようになります(e.g., H1: mu1 < (mu2 = mu3))。
complexH (3,1,1)
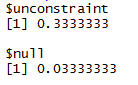
このコードを走らせるとこんな結果が返ってきます。
差がないと考える変数について,積極的に同じであるかを検討したい場合は`null`の結果を,特に同じであるという仮定をしない場合は`unconstraint`の結果を仮説の複雑性として使うとよいでしょう。Hoijtink, Klugkist, Boelen (2010)のハンドブックの中では,両方やってみて比較したらよいようなことが書いてあったと思います。