はじめに
この記事は,Stan advent calendar 2018の最終日の記事です。つまり,クリスマスの記事ですね。みなさんは何をされているでしょうか。私はクリスマスプレゼントに査読依頼と学生から卒論のためにとったデータをいただきました。
それと,この記事は,昨年から続くM-1データを解析するシリーズの続編です。今年のStan advent calendar 2018の初日と4日目にも記事にもなっていますし,昨年の取り組みはなんと本にもまとまっています。興味のある方はそちらもご覧ください。
M-1グランプリに関してちょこっとネットサーフィンすると,こんな感じの記事がひっかかったりして,つまり,吉本興業(よしもとクリエイティブエイジェンシー含む。)の芸人ばかり出場しているじゃないか,というような内容が書かれているわけです(e.g., 吉本芸人だらけの「M-1グランプリ」に東京勢からあがった“反旗”の声
, 『M-1』準決勝進出者が大阪よしもと勢ばかりでブーイング 東京芸人の間では「もう出る必要はない」)。昨日Netflixで第1回のM-1グランプリを見ていたのですが,少なくとも第1回大会の当時の大会運営委員長の島田紳助氏は,事務所は関係ないガチンコだというようなことを言ってました。
この記事は,この初期の運営にみられた発言通りに採点されていたのか,つまり,演者の所属する事務所グループ(以下では,事務所)によって評価得点に偏りがないかを検討してみたよ,というものになっています。最近,私のネットサーフィンによる観測範囲で確認できたM-1で吉本勢ばかりだ,というものを検証するものにはなっていません。
なお,今回の推定では,事務所にって偏りがあったとしても,その事務所に所属する演者たちが,他の事務所よりも単純に上手い集団である可能性は否定できません。今回,演者たちの事務所を調べる中で,途中で事務所を変わる演者もいて,その理由により多くの経験を積むため(Wikipediaに書かれていたことで,真偽まではわかりませんが),といったものもありました。なので,特定の事務所の得点が高いといった結果が得られたときに,それがその事務所特有の訓練などによるといった可能性も考えられます。劇場が多いとその分,ネタをする機会も多いらしいのでそういったこともあるかもしれません。
データ作成とその他準備
データ作成をします。基本は,昨年使用したデータにM-1グランプリ2018のデータを足し,出場時に所属していた事務所と出演順序を調べて追加していきました。データはここに置いておきます(OSF)。
まずは,解析などに使うパッケージを読み込んでおきます。今回,使用したのは以下ものになります。
Sys.setlocale(category="LC_ALL", locale="ja_JP.UTF-8") library(rstan) library(brms) library(tidyverse) library(tidybayes) library(bayesplot) library(ggridges) rstan_options(auto_write = TRUE) options(mc.cores = parallel::detectCores())
データを読み込み,変数名を半角に全て変えておきます。それと,今回は,評価者と事務所の組み合わせの効果を見ておきたいので,その組み合わせの変数(int_ro)も作っておきます。
# データ読み込み & 変数作成----
dat <- read_csv("m1_score_2018.csv",
locale = readr::locale (encoding = "Shift_JIS")
)
dat01 <- dat
dat01$val_z <- scale(dat$val)
head(dat01)
## 変数名を半角にしよう
col <- c("year", "player", "rater", "val", "order", "office", "val_z")
colnames(dat01) <- col
## 評価者*事務所の組み合わせの変数を作成
dat01$int_ro <- str_c(dat01$rater, dat01$office, sep = "_")
番外:ランダム切片モデルの交互作用をどう書けばよいのかの確認
試したいモデルは,混合モデルでいうところのランダム切片モデルの,ランダム切片間の交互作用を検討するものになります。いまいちStanでどう書いたらよいのかわからずにいたのですが(特に変数間の相関を仮定したりは今の私にはけっこうしんどい),brmsパッケージを使うと,ランダム切片間の交互作用も検討できそうでした。
brmsパッケージは,lme4パッケージとほとんど同じ記法でベイズ推定が使える大変便利なパッケージです。ランダム効果をみたいときには,(1|hoge)とすればよいわけですが,複数ある場合には,(1|hoge) + (1|huga)と書いたり,同じことが(1|hoge + huga)でもできます。このランダム効果同士の交互作用を見る場合は,(1|hoge:huga)でいけるようです。今回は,brmsでのモデルをmake_stancode()とdata_stan()を用いて,StanコードとそのStanに送るデータセットを作成して,どのようにStanで書いたら良いかを考えてみました。長いので省略しますが,brmsの場合でも,Stanに送るデータを作る段階でランダム効果間の交互作用項を作成しているようでした。
### 番外編: ランダム切片モデルの交互作用をどう書けばよいのかの確認
make_stancode(formula = val_z ~ (1 | player + rater + office) + (1 | rater:office),
data = dat01)
data_stan <- make_standata(formula = val_z ~ (1 | player + rater + office) + (1 | rater:office),
data = dat01)
事務所別出演回数
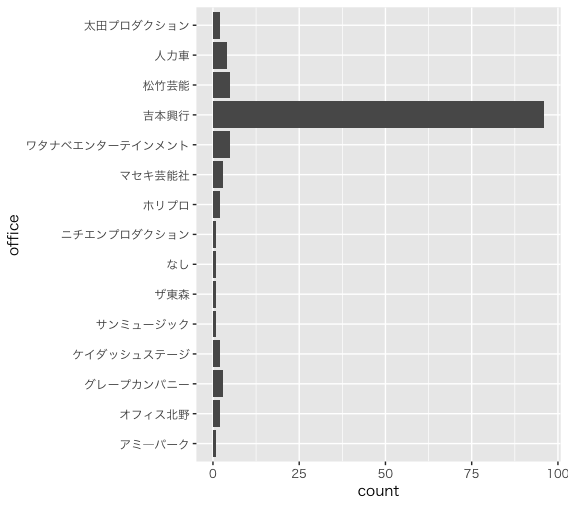
M-1グランプリの決勝に残った回数を事務所ごとに算出し,可視化してみます。コードはこんな感じです。1行目はMacで日本語が豆腐にならないようにする呪文です。以下のような図ができます。
theme_set(theme_gray(base_family="HiraKakuProN-W3")) dat01 %>% distinct(year, player, office) %>% group_by(office) %>% summarize(count = n()) %>% arrange(desc(count)) %>% ggplot(aes(x = office, y = count)) + geom_bar(stat = "identity") + coord_flip()
思っていたよりも吉本興業の人が多かったです。お笑いコンビの総数のうち,吉本興業がどのくらいを占めているのかはわかりませんがM-1グランプリにおいては圧倒的ですね。他の事務所は,まだ,10組も決勝に残っていません。なお,なしは所属事務所なしのことを指しています。
解析してみる
以下では,これまでM-1グランプリのデータをいろいろと使って推定していきます。
モデルの説明
今回のモデルは,基本ベースとして昨年のものを用いながら,出演順序と事務所,評価者と事務所の交互作用をモデルに追加していきます。確率モデルは以下のようになります。出演順序の効果に関しては,今年のStanアドカレ初日小杉さんの考えられたモデルのほうが明らかに綺麗だと思うのですが,今回は特に制約を設けずにやってみます。
また,事務所による評価の偏りを見るのが目的ですが,ある評価者は特定の事務所を高評価しやすいといった可能性も考えられます。この評価者と事務所の交互作用も今回は検討していきます。
$$X_{ijz} \sim Normal(\theta_{player} + \theta_{rater} + \theta_{order} + \theta_{office} + \theta_{rater*office}, \sigma) \\
\theta_{player} \sim Normal(0, \sigma_{theta_{player}}) \\
\theta_{rater} \sim Normal(0, \sigma_{theta_{rater}}) \\
\theta_{order} \sim Normal(0, \sigma_{theta_{order}})\\
\theta_{office} \sim Normal(0, \sigma_{theta_{office}}) \\
\theta_{rater*officr} \sim Normal(0, \sigma_{theta_{rater*officr}}) \\
\sigma \sim cauchu(0, 5)$$
これをStanに書き下すとこんな感じになると思います。もう変数が多くなりすぎて,以前のように$\tau$とかつけられなくなりました。$\theta_{player}$も全て書いていると面倒になって,順にAから振っていっています。
data{
int<lower=1> A; //data Length
int<lower=1> B; //number of players
int<lower=1> C; //number of raters
int<lower=1> D; //number of year
int<lower=1> E; //number of office
int<lower=1> F; //number of order
int<lower=1> CE; //number of rater*office
int idB[A]; //player ID index
int idC[A]; //rater ID index
int idD[A]; //year ID index
int idE[A]; //office ID index
int idF[A]; //order ID index
int idCE[A]; //rater*office ID index
real Y[A]; // scores
}
parameters{
vector[B] thetaB; //manzai
vector[C] thetaC; //rater
vector[D] thetaD; //year
vector[E] thetaE; //office
vector[F] thetaF; //order
vector[CE] thetaCE; //rater*office
real<lower=0> sig_thetaB;
real<lower=0> sig_thetaC;
real<lower=0> sig_thetaD;
real<lower=0> sig_thetaE;
real<lower=0> sig_thetaF;
real<lower=0> sig_thetaCE;
real<lower=0> sig_e;
}
model{
//likellihood
for(i in 1:A){
Y[i] ~ normal(thetaB[idB[i]] + thetaC[idC[i]] + thetaD[idD[i]] + thetaE[idE[i]] + thetaF[idF[i]] + thetaCE[idCE[i]] , sig_e);
}
//prior
thetaB ~ normal(0, sig_thetaB);
thetaC ~ normal(0, sig_thetaC);
thetaD ~ normal(0, sig_thetaD);
thetaE ~ normal(0, sig_thetaE);
thetaF ~ normal(0, sig_thetaF);
thetaCE ~ normal(0, sig_thetaCE);
sig_thetaB ~ cauchy(0,5);
sig_thetaC ~ cauchy(0,5);
sig_thetaD ~ cauchy(0,5);
sig_thetaE ~ cauchy(0,5);
sig_thetaF ~ cauchy(0,5);
sig_thetaCE ~ cauchy(0,5);
sig_e ~ cauchy(0,5);
}
generated quantities{
real rho_player;
real rho_rater;
real rho_order;
real rho_office;
rho_player = sig_thetaB^2 / (sig_thetaB^2 + sig_thetaC^2 + sig_thetaE^2 + sig_thetaF^2 + sig_thetaCE^2 + sig_e^2);
rho_rater = sig_thetaC^2 / (sig_thetaB^2 + sig_thetaC^2 + sig_thetaE^2 + sig_thetaF^2 + sig_thetaCE^2 + sig_e^2);
rho_order = sig_thetaE^2 / (sig_thetaB^2 + sig_thetaC^2 + sig_thetaE^2 + sig_thetaF^2 + sig_thetaCE^2 + sig_e^2);
rho_office = sig_thetaF^2 / (sig_thetaB^2 + sig_thetaC^2 + sig_thetaE^2 + sig_thetaF^2 + sig_thetaCE^2 + sig_e^2);
}
55行目以降のgenerated quantitiesブロックについて簡単に説明します。
- 56-59行目:rho_hogeという4つの信頼性のパラメタを計算するようにしています。
- 60行目:演者の信頼性。1回の大会における分散成分のうち,演者の分散が占める割合を計算
- 61行目:評価者の信頼性。1回の大会における分散成分のうち,評価者の分散が占める割合を計算
- 62行目:順序の信頼性。1回の大会における分散成分のうち,出演順序の分散が占める割合を計算
- 63行目:事務所の信頼性。1回の大会における分散成分のうち,事務所の分散が占める割合を計算
これを”model01.stan”と名前をつけて保存して,走らせます。Stanに渡すデータについては,以下のようにしています。
datastan01 <- list(A = nrow(dat01), # 全体の数
B = length(unique(dat01$player)), # 演者の数
C = length(unique(dat01$rater)), # 評価者の数
D = length(unique(dat01$year)), # 開催回数の数
E = length(unique(dat01$office)), # 事務所グループの数
F = length(unique(dat01$order)), # 順序の数
CE = length(unique(dat01$int_ro)), # 評価者と事務所の組み合わせの数
idB = as.numeric(as.factor(dat01$player)), # 演者の識別
idC = as.numeric(as.factor(dat01$rater)), # 評価者の識別
idD = as.numeric(as.factor(dat01$year)), # 開催回数の識別
idE = as.numeric(as.factor(dat01$office)), # 事務所グループの識別
idF = as.numeric(as.factor(dat01$order)), # 順序の識別
idCE = as.numeric(as.factor(dat01$int_ro)), # 評価者と事務所の組み合わせの識別
Y = as.numeric(dat01$val_z) # 標準化された評価得点
)
Stanを走らせるコードはこんな感じです。
model01 <- stan_model("model01.stan") # model01.stanのファイルをコンパイルし,model01として読み込む
fit01 <- sampling(model01, # model01のモデルを使用
data = datastan01, # datastan01のデータを使用
iter = 10000, # 1チェインのサンプリング回数
chains = 4 # チェインの数
)
収束の確認
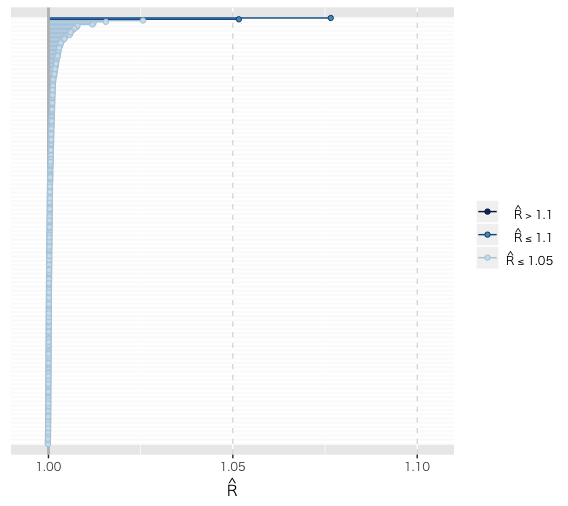
Stanアドカレ2日目の北條さんの記事を参考に,bayesplotパッケージを使用して収束の確認をしてみます。
mcmc_rhat(rhat(fit01))
Rhatは少し怪しい部分もありますが,.10を超えたものはなさそうですし,だいたい大丈夫そうです。可視化すると数値を見るよりも見落としが少なくなって良さそうですね。
事務所により評価の偏りはあるのか
長くなってますが,本題に入ります。事務所によって評価に偏りがあるかをみてみます。Stanアドカレ3日目の竹林さんの記事を参考に,tidybayesパッケージを使って,こんな感じのコードで可視化までもっていってます。可視化が苦手だったのでだいぶアドベントカレンダーに救われています。ありがとうStanアドカレ。
office_name <- levels(as.factor(unique(dat01$office))) %>%
data.frame() %>%
add_rownames(var = "E") %>% # 行番号を列名"E"の変数としてデータフレームに加える
dplyr::rename(office = ".") # 事務所のデータが入った列名が"."となっているので"office"に変更
office_name$E <- as.integer(office_name$E) # 行番号は文字列として読み込まれているので整数に変更
fit01_office <- fit01 %>%
spread_draws(thetaE[E])
fit01_office <- left_join(fit01_office, office_name, by = "E")
theme_set(theme_gray(base_family="HiraKakuProN-W3")) # Macで日本語が豆腐にならないための呪文
fit01_office %>%
ggplot() +
stat_pointintervalh(aes(y = as.factor(office),
x = thetaE),
point_interval = mode_hdci, # 最頻値を使って最高確率区間をマーク
.width=c(.90, 0.95)) + # 指定したパーセンテージの区間を表示。今なら90%HDIと95%HDI
ylab(label = "事務所") +
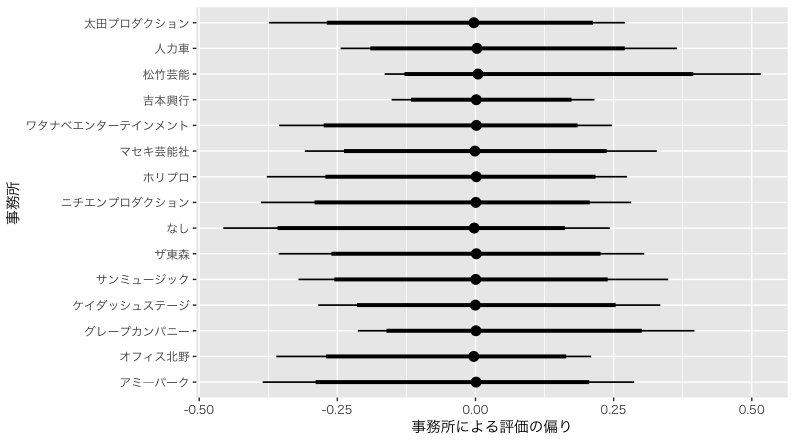
xlab(label = "事後HDI")
最頻値でみるとほとんど違いがありませんでした。区間推定値をみると,データ数が多いこともあってか,吉本興業はかなり幅がせまく推定されていますね。少なくとも,M-1グランプリの決勝の得点には吉本びいき,のようなことはなさそうです。他の事務所は出場者が少ないことも影響していそうですが,松竹芸能が高く評価される可能性が若干高いようにも見えます。
評価者と事務所の組み合わせによる影響
事務所による評価得点の違いはほとんどなさそうでした。ただ,評価者によっては事務所による評価得点の違いが出てくる可能性もあります。同じ事務所だと,漫才をみるケースがあり,親近性によって評価してしまうこともあるかもしれません。
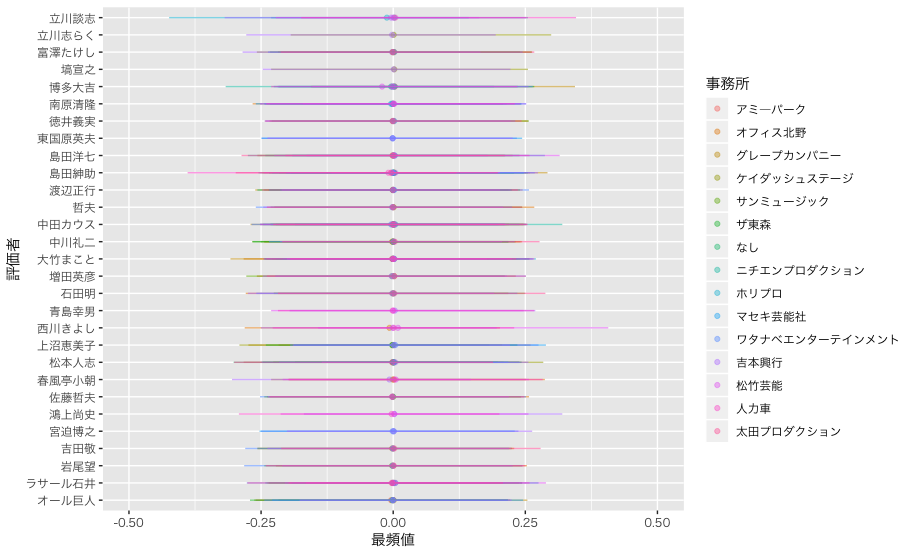
全部の数値を出すと長くなってしまうので,以下に評価者ごとの事務所による評価得点の区間推定値を示します。点は,最頻値です。わかりずらいかもしれませんが,薄くして透けるようにしているので,事務所によらず評価が一定であれば,色が濃く見えるようにしてみました。
区間推定値でみると,立川談志氏や西川きよし氏の区間推定値が事務所によって異なるケースがあるようです。しかし,最頻値をみるとほとんど変わらないですねー。いやー審査員のみなさん本当に平等に評価されている様子がわかります。
その他の結果
出演順序による違い
出演順序による評価得点の違いをみてみます。
> fit01_order
# A tibble: 10 x 7
順序 最頻値 .lower .upper .width .point .interval
<int> <dbl> <dbl> <dbl> <dbl> <chr> <chr>
1 1 -0.178 -0.428 0.0511 0.95 mode hdci
2 2 -0.424 -0.698 -0.211 0.95 mode hdci
3 3 -0.288 -0.539 -0.0338 0.95 mode hdci
4 4 0.0961 -0.135 0.319 0.95 mode hdci
5 5 0.181 -0.0546 0.420 0.95 mode hdci
6 6 0.138 -0.0841 0.386 0.95 mode hdci
7 7 -0.0279 -0.245 0.224 0.95 mode hdci
8 8 0.0293 -0.202 0.269 0.95 mode hdci
9 9 0.185 -0.0619 0.417 0.95 mode hdci
10 10 0.219 -0.0614 0.601 0.95 mode hdci
2番目と3番目は評価得点が低くなりやすいようですね。後半は全体的にプラスに向かいやすいようですが,明確な影響は出ていませんね。やはり相対的に比較するようなモデルのほうがよかったかなー。
演者の真のおもしろさ(仮)
あと開催回数の効果をとばしていますが,これらを統制した場合の演者のおもしろさがどうなるかをみてみましょう。
中川家,ますだおかだ,フットボールアワー,ブラックマヨネーズ,アンタッチャブルと続いています。昨年の結果からあまり大きく変わっていないところをみると,開催回数による補正が大きそうですね。
1回のM-1グランプリの評価得点の構成要素
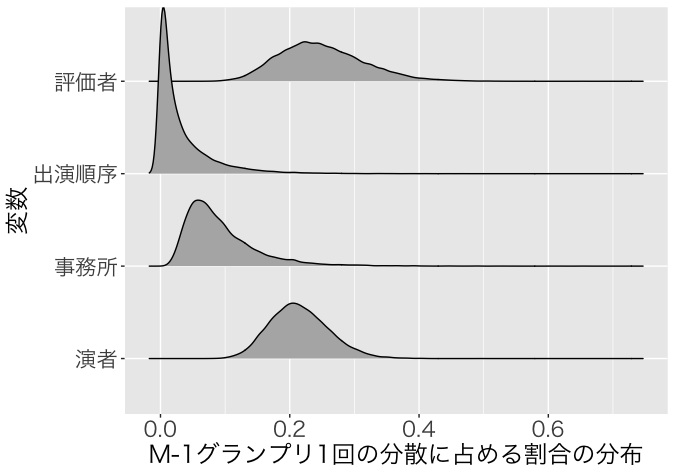
最後に,1回のM-1グランプリの評価得点の構成要素のうち,事務所,順序,評価者,演者のおもしろさはどの程度影響しているかみてみましょう。それぞれの分散成分を推定しているので,評価得点のうち何割くらい説明できるかをみてみます。ggridgesパッケージのgeom_density_ridgesを使ってまとめてみたいと思います。
fit01 %>% print(pars=c("rho_player", "rho_rater", "rho_order", "rho_office"))
fit01_rho <- fit01 %>%
spread_draws(rho_player, rho_rater, rho_order, rho_office) %>%
gather(key = names, value = rho, rho_player:rho_office)
str(fit01_rho)
fit01_rho$names <- as.factor(fit01_rho$names)
levels(fit01_rho$names)
fit01_rho$names_num <- as.numeric(fit01_rho$names)
rho_name_list <- data.frame(names = c("rho_office", "rho_order", "rho_player", "rho_rater"),
labels = c("事務所", "出演順序", "演者", "評価者"))
fit01_rho01 <- left_join(fit01_rho, rho_name_list, by = "names")
ggplot(fit01_rho01) +
geom_density_ridges(aes(x = rho, y = as.factor(labels))) +
xlab(label = "M-1グランプリ1回の分散に占める割合の分布") +
ylab(label = "変数") +
theme(axis.text.y = element_text(size = 16),
axis.title.y = element_text(size = 18),
axis.title.x = element_text(size = 18),
axis.text.x = element_text(size = 16))
評価者と演者のおもしろさは2割を超えてますが,出演順序と事務所の効果は1割きってますね。特に順序の効果の説明率は低いようです。事務所の効果は目立った影響がなかったわりに順序よりも説明率が高いのが少し不思議です。
まとめと反省
事務所による評価の偏りがないかをみてみましたが,思っていた以上に推定値がずれておらず驚きました。こんな風に思ったことを気軽に自分で検証できるのがよいですね。
このモデルには不十分な点が多く,まだまだ改善の見込みがあります。すぐにできそうなこととしては,100点近くは出にくいと考え,シグモイド関数をかませるとか,これは学会で指摘された点ですが,出やすいキリのよい点数をどうモデリングするのかといった点です。また,このモデルには固定効果が入っていないのが,モデルとしてはうーんとなってしまっています。ビデオみながら,笑い声の大きさとかを説明変数にしてみようかな,と思っています。
俺たちのモデリングはこれからだ!ということで最終回風に終わりたいと思います。ここまでご笑覧いただきありがとうございます。