この記事は,Stan advent calendar 2018の9日目の記事です。カイ2乗検定のようなことをStanでやってみようという内容です。何か致命的な間違いがあれば教えていただければと思います。
パッケージの読み込みなど
まずはパッケージの読み込みから。
library(rstan) options(mc.cores = parallel::detectCores()) rstan_options(auto_write = TRUE)
実行環境の状態確認(macOS Mojaveのlocale問題の解決)
今回,この記事を書くための解析を行なった環境を紹介します。
sessionInfo()
R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS 10.14.1
Matrix products: default
BLAS: /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] C
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] rstan_2.17.3 StanHeaders_2.17.2 ggplot2_3.1.0
[後略]
rstan2.18にしていないことがばれますね。。それとlocaleが見慣れないものになっています。
macOSをMojaveにアップデートしてからデータの読み込みがおかしいことあったので,確認してみるとlocale: Cとなっていました。調べてみると,Rstudioのコミュニティにこんな情報が。日本語だけの問題でもなかったようです。みんな困ってたんですね。
というわけで,localeをUTF-8と日本語を読み込めるように呪文を走らせて変更しておきます。
Sys.setlocale(category="LC_ALL", locale="ja_JP.UTF-8") sessionInfo()
R version 3.4.3 (2017-11-30)
Platform: x86_64-apple-darwin15.6.0 (64-bit)
Running under: macOS 10.14.1
Matrix products: default
BLAS: /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
locale:
[1] ja_JP.UTF-8/ja_JP.UTF-8/ja_JP.UTF-8/C/ja_JP.UTF-8/C
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] rstan_2.17.3 StanHeaders_2.17.2 ggplot2_3.1.0
[後略]
ちゃんとlocaleが変わっていることが確認できます。これでいつも通りにデータの読み込みなどができるはず。それでは,よいRライフを。これでR advent calendar 2018の9日目の記事を終わります。
嘘です。これはStan advent calenderなので,ちゃんと?Stanを使います。続きます。本当のR advent calendar 2018はこちら
カイ2乗検定的なことがしたい
さて本題です。カイ2乗検定的なことをしていきます。でも,実は,カイ2乗検定をベイジアンモデリングでやってみるというものはすでにTJOさんが試されています。
p値を計算したくなる検定の数々を試しにStanによるベイジアンモデリングで代替してみた
今回は,TJOさんの記事をもとに,ほとんど同ことをやってみます。私のようなプログラミングに弱い人間は,Stanコードだけ見ていると,やっていることがわからなくなってしまうことが多いので,Stanコードの中身を極力シンプルにして,自分用の解説をしていこうかと思います。
データの準備
今回のデータはJamil, Ly, Morey, Love, Marsman, & Wagenmakers (2017)の中で紹介されているAnderson (1990)のデータでやってみます。デンマークの労働者の満足度(低,高)とスーパーバイザーの満足度(低,高)の人数の関係を調べたもののようです。データは以下のような感じです。
dat <- data.frame(w_low_s = c(162, 110), # w_low_s: Worker low satisfaction
w_high_s = c(196, 247), # w_high_s: Worker high satisfaction
sv_s = c("low", "high")) # sv_s: Supervisor satisfaction
dat$sv_s <- relevel(dat$sv_s, "low")
dat

- 1行目:低い満足度の労働者数。スーパーバイザーの満足度が低い場合162名,高い場合110名
- 2行目:高い満足度の労働者数。スーパーバイザーの満足度が低い場合196名,高い場合247名
- 3行目:スーパーバイザーの満足度の高低。
- 4行目:このまま数値化すると,highが1,
lowが2となる。lowを1とし,highを2として,参照点をlowにするためのコード。
Stanに渡すデータはこんな感じにします。
dat_stan <- list(N = 2,
low = dat$w_low_s,
high = dat$w_high_s,
sv = as.numeric(dat$sv_s))
- 1行目:Nは分割表の行数。今回はスーパーバイザーの満足度(高,低)の2行のためN = 2
- 2行目:満足度の低い労働者数(w_low_s)をlowに格納
- 3行目:満足度の高い労働者数(w_high_s)をhighに格納
- 4行目:factor型のスーパーバイザーの満足度(low, high)を数値型(low = 1, high = 2)に変換
カイ2乗検定的なことを行うStanコード
TJOさんによると,こんな感じの表を分析する場合,二項ロジット分析の枠組みを使うとのことで,今回の場合はこんなモデルになるようです。
$$Worker High Satisfaction \sim Binomial(Worker High Satisfaction+Worker Low Satisfaction, p) $$
$$p = exp(a + bx) / 1 + exp(a+bx)$$
高い満足度の労働者は,労働者全体(高い満足度の労働者 + 低い満足度の労働者)のうち,確率pで生じる。そして,確率pは,よくある回帰分析の予測値を確率に返すようにしている処理(たしか逆ロジット変換でよいはず)を行なっています。この辺りがロジット分析の枠組みな感じでしょうか。
これをStanコードに書き下します。下記のStanコードを”chi2_binomial01.stan”として作業ディレクトリに保存します。
data {
int<lower=0> N;
int<lower=0> low[N];
int<lower=0> high[N];
real<lower=1,upper=2> sv[N];
}
parameters {
real a;
real b;
}
model {
real p[N];
p[1] = inv_logit(a + b*sv[1]);
p[2] = inv_logit(a + b*sv[2]);
for (i in 1:N){
high[i] ~ binomial(low[i] + high[i], p[i]);
}
}
generated quantities {
real pp[N];
real diff_pp;
pp[1] = inv_logit(a + b*sv[1]);
pp[2] = inv_logit(a + b*sv[2]);
diff_pp = pp[2] - pp[1];
}
- 2-5行目:リスト型にしたデータをStanに渡す
- 9, 10行目:推定するパラメタaとb
- 14行目:pというパラメタを推定
- 15行目:低い満足度のスーパーバイザーにあたる労働者のデータで逆ロジット変換をする
- 16行目:高い満足度のスーパーバイザーにあたる労働者のデータで逆ロジット変換をする
- 17-19行目:全労働者(低満足+高満足)の中で,確率pで高い満足度の労働者が生じる二項分布の生成メカニズムを仮定する
- 24, 25行目:推定結果を用いて新たにppをN個とdiff_ppという変数を算出する
- 25行目:pp[1]としてスーパーバイザーの満足度が低い群での労働者の満足度が高い群となる事後確率を算出
- 26行目:pp[2]としてスーパーバイザーの満足度が高い群での労働者の満足度が高い群となる事後確率を算出
- 27行目:diff_ppとしてスーパーバイザーの満足度の高い群の事後確率(pp[2])と低い群の事後確率(pp[1])の差分を算出。スーパーバイザーの満足度によって満足度の高い労働者が増えるか検討する
さあ推定だ
あとは推定するだけ。
fit <- stan(file = "chi2_binomial01.stan",
data = dat_stan)
fit
traceplot(fit)
- 1, 2行目:MCMC(;´Д`)ハアハア
- 3行目:ざっと結果の確認
- 4行目:トレースプロットの確認
Inference for Stan model: chi2_binomial01.4 chains, each with iter=2000; warmup=1000; thin=1; post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
a -0.43 0.01 0.25 -0.94 -0.61 -0.44 -0.25 0.05 698 1
b 0.62 0.01 0.16 0.31 0.51 0.62 0.73 0.94 685 1
pp[1] 0.55 0.00 0.03 0.49 0.53 0.55 0.57 0.60 1023 1
pp[2] 0.69 0.00 0.02 0.64 0.68 0.69 0.71 0.74 1387 1
diff_pp 0.14 0.00 0.04 0.07 0.12 0.15 0.17 0.22 681 1
lp__ -468.04 0.03 1.05 -470.89 -468.42 -467.72 -467.31 -467.04 999 1
Samples were drawn using NUTS(diag_e) at Sun Dec 9 23:23:53 2018.For each parameter, n_eff is a crude measure of effective sample size,and Rhat is the potential scale reduction factor on split chains (at convergence, Rhat=1).
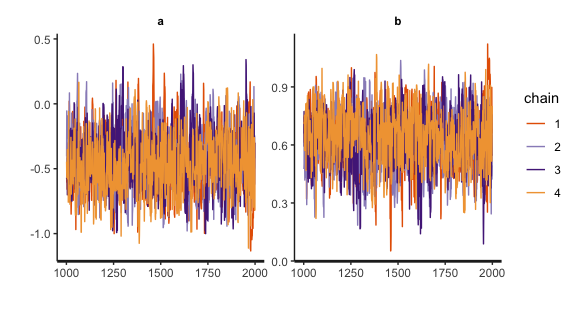
無事に収束しているようですし,bの区間推定値も0を挟んでいないので,労働者の満足度高低で人数の違いはあるいってよさそうです。diff_ppも区間推定値に0を挟まないので,スーパーバイザーの満足度によっても満足度の高い労働者数も増えると言えそうです。一応bの推定値を可視化しておきましょう。
fit_b <- rstan::extract(fit)$b %>% transform()
colnames(fit_b) <- "b"
q_lower <- quantile(fit_b$b, probs = 0.025) # 95%信用区間の下限を算出
q_upper <- quantile(fit_b$b, probs = 0.975) # 95%信用区間の上限を算出
dens <- density(fit_b$b)
dens_df <- data.frame(b = dens$x, density = dens$y)
g01 <- ggplot(data = dens_df, aes(x = b, y = density))
g01 <- g01 + geom_line(size = 0.7)
g01 <- g01 + geom_ribbon(data = subset(dens_df,
b >= q_lower & b <= q_upper),
aes(x = b, ymin=0, ymax = density), fill = "black", alpha = 0.4
)
g01 <- g01 + labs(x = expression(italic(b)))
g01 <- g01 + theme(axis.text = element_text(size = 16),
axis.title = element_text(size = 18)
)
g01
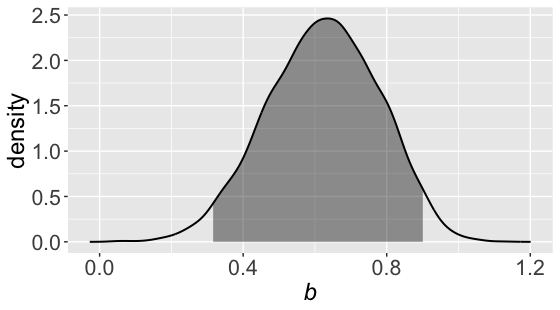
Enjoy Stan!
反省文
この記事は二番煎じに過ぎず,さらに本来自分でちゃんと確認すべきことが確認しきれておりません。記事にしたものの,なんかもやもやしていてところがあって,まだ理解できた!という感じがありません。
本当は5*6の分割表に対して,多項分布を使ったり,JASPでBayes factorを出してくれるので,それをStanで再現し,かつ,残差分析までやってみたり,ということにチャレンジしたかったので,分割表をJASPやBayesFactorパッケージでどのように求めているか書かれた論文を読んでいたのですが,サンプルコードがあったrjags試しにやったら推定途中でRstudioがアボーンするし,いろいろと迷子になってしまって今回は諦めました。明らかに鍛錬不足,,,がんばります。