Stanのアドカレ,毎日楽しいですね。
あるStanアドカレの投稿をきっかけとして一部である議論が巻き起こりました。
それは”いったい誰が最強のM-1漫才師なのか”ということです
私が投稿に至るまでの少し流れを整理します。
きっかけは2017/12/11担当の山口大学の小杉先生の最強のM-1漫才師は誰だです。
そこでこんなことを主張されていました。
ブラマヨが一番すごいんじゃないか
出典:Kosugitti Lab ver9.0 最強の漫才師は誰だ(http://kosugitti.net/archives/6261)
さらにTwitterでこんな感じに煽っております。
データも公開してますので、結果に納得のいかない人は再分析してみてね! https://t.co/7POC81w4dE
— kosugitti (@kosugitti) 2017年12月10日
そんなTweetに触発された方が一人。
関西学院大学の清水先生でした。
今日の@kosugitti さんのアドカレ記事に触発されて,僕も最強のM-1漫才師が誰かMCMCで推定してみました。僕のモデルだと,なんとあの漫才師が・・・
他にもチャレンジする人がいればぜひ!https://t.co/AaMnh9Gtqj— Hiroshi Shimizu (@simizu706) 2017年12月11日
ネタバレ(?)になりますが,清水先生の解析モデルでは以下のように結論づけています。
小杉さんの記事ではブラマヨが最強,ということでしたが,採点者の甘さを考慮に入れるとパンクブーブーがトップとなりました。
出典:Sunny side up! 「最強のM-1漫才師は誰だ」 へのチャレンジ(norimune.net/3093)
どうもお二人とも新たなモデルによる再解析をしてくる挑戦者を待っているようなので,私もノリで参戦してみようと投稿になります。
小杉モデルの確認
清水先生が小杉先生のモデルを整理してくださっているので,それを引用します。
小杉さんのモデルは,採点者の「採点のばらつき」をモデリングしています。ある漫才への評価は,その漫才師の漫才力に,評価のばらつきが加味されているだろう,というわけです。漫才師iが,採点者jに採点されたときの得点Xは,漫才力θを平均,採点者のバラ付きσを標準偏差とした確率分布に従うだろう,というわけです。
確率モデルは,以下のように示されています。
$$X_{ij} \sim Normal(\theta_i, \sigma_j)$$
清水モデルの確認
清水先生のモデルは,「最強のM-1漫才師は誰だ」 へのチャレンジにおいて,以下のように説明されています。
小杉さんのモデルで不満点があるとすれば,採点者の甘さが考慮されてないところです。例えば上沼恵美子は全体的に甘いけど,博多大吉は厳しい,とかです。このように採点者の採点の甘さが正規分布に従うような階層モデルを考えてみます。
まず,採点結果は,全体平均+漫才力+採点者の甘さを平均とした正規分布に従うとします。漫才力,採点者の甘さは平均0の正規分布に従うと仮定します。ただ,分散は推定します。
確率モデルは以下のように示されています。
$$X_{ij} \sim Normal(mu + \theta_i + \gamma_j, \sigma) \\
\theta_i \sim Normal(0, \sigma_{\theta}) \\
\gamma_j \sim Normal(0, \sigma_{\gamma})$$
大会の開催された年代の効果を変量効果として推定する
ここからが本題です。私は,この清水先生のモデルにさらに,大会の開催された年代の効果を変量効果として推定していきます。最近のM-1って高得点多くないですか?というか低得点が少なくなったといいますか。大吉先生はそのあたりのことについて,評価基準や大会出場の規定が代わり,ベテランの域に達している人たちまで出られるようになったからだとおっしゃっていましたが(博多大吉のM-1審査員をやって・・・https://radiocloud.jp/archive/tama954/?content_id=24438)。
清水先生の指摘するように「採点者の甘さ」もあるとは思うのですが,「年代ごとに採点の特徴」があるのではないかと思うのです。特に,最初の頃の大会は,まだ評価基準が今ほど明確でなかった可能性もありますし,エンターテイメントとして大会を改善していこうとする中で評価基準が変わっていくことだってありうるわけです。こうしたことを考慮すると,初期のM-1は,今と比べると漫才力に対して不当に点数が低い可能性が考えられます。今回のモデルは,このような年ごとの採点の特徴が正規分布に従うような階層モデルを考えてみます。
つまり,\(採点結果_{ijz}は全体平均 + 漫才力_i + 採点者の甘さ_j + 年代の特徴_z\)を平均とした正規分布に従うとします。漫才力,採点者の甘さ,年代の特徴は平均0の正規分布に従うと仮定します。清水先生のモデルと同様に分散も推定します。確率モデルは以下のようになります。
$$X_{ijz} \sim Normal(mu + \theta_i + \gamma_j + \tau_z, \sigma) \\
\theta_i \sim Normal(0, \sigma_{\theta}) \\
\gamma_j \sim Normal(0, \sigma_{\gamma}) \\
\tau_z \sim Normal(0, \sigma_{\tau})$$
Stanコードは以下に示すものを使用しました。
data{
int<lower=1> L; //data Length
int<lower=1> N; //number of players
int<lower=1> M; //number of rators
int<lower=1> O; //number of year
int idX[L]; //player ID index
int idY[L]; //rator ID index
int idZ[L]; //year ID index
real X[L]; // scores
}
parameters{
real mu;
vector[N] manzai;
vector[M] saiten;
vector[O] year;
real<lower=0> sig_manzai;
real<lower=0> sig_saiten;
real<lower=0> sig_year;
real<lower=0> sig;
}
model{
//likellihood
for(l in 1:L){
X[l] ~ normal(mu + manzai[idX[l]] + saiten[idY[l]] + year[idZ[l]],sig);
}
//prior
manzai ~ normal(0, sig_manzai);
saiten ~ normal(0, sig_saiten);
year ~ normal(0, sig_year);
sig_manzai ~ cauchy(0,5);
sig_saiten ~ cauchy(0,5);
sig_year ~ cauchy(0,5);
sig ~ cauchy(0,5);
}
これを”m1_tokuoka.stan”と名前をつけて保存して,走らせます。データについては,元のデータやロング型に変えた時のデータは,小杉先生,清水先生と同様ですが,年代を変量効果として推定するため,以下のようにStanに年代に関するデータも渡すようにしています。
datastan <- list(L=nrow(m1.long),
N=max(as.numeric(m1.long$演者)),
M=max(as.numeric(m1.long$審査員)),
O=max(as.numeric(m1.long$年代)), #NEW VARIABLE
idX=as.numeric(m1.long$演者),
idY=as.numeric(m1.long$審査員),
idZ=as.numeric(m1.long$年代), #NEW VARIABLE
X=m1.long$val
)
Stanを走らせるコードはこんな感じ(清水先生の丸パクリ)。
model.tokuoka <- stan_model("m1_tokuoka.stan")
fit.tokuoka <- sampling(model.tokuoka,data=datastan,iter=2000,chains=2,cores=1)
結果は,以下のようになります。まずは,漫才力から,ちゃんと収束しているようです。
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat manzai[1] 2.14 0.04 1.63 -1.02 1.03 2.13 3.22 5.35 2000.00 1 manzai[2] -0.39 0.04 1.65 -3.52 -1.51 -0.38 0.75 2.89 2000.00 1 manzai[3] 2.07 0.03 1.29 -0.54 1.23 2.06 2.93 4.59 2000.00 1 manzai[4] -4.27 0.03 1.14 -6.42 -5.04 -4.26 -3.53 -1.92 2000.00 1 manzai[5] -0.04 0.04 1.60 -3.21 -1.08 0.00 0.98 3.12 2000.00 1 manzai[6] -0.91 0.04 1.92 -4.65 -2.24 -0.93 0.34 3.09 2000.00 1 manzai[7] -4.92 0.04 1.62 -8.14 -5.97 -4.91 -3.82 -1.78 2000.00 1 manzai[8] -0.28 0.02 1.11 -2.40 -1.06 -0.28 0.49 1.86 2000.00 1 manzai[9] 5.06 0.03 1.28 2.59 4.23 5.04 5.90 7.58 2000.00 1 manzai[10] 2.78 0.04 1.65 -0.46 1.67 2.78 3.87 6.03 2000.00 1 manzai[11] -1.07 0.03 1.31 -3.73 -1.94 -1.06 -0.17 1.41 2000.00 1 manzai[12] -3.83 0.04 1.68 -7.08 -4.94 -3.83 -2.67 -0.63 2000.00 1 manzai[13] 0.50 0.04 1.65 -2.74 -0.64 0.54 1.63 3.68 2000.00 1 manzai[14] -2.05 0.03 1.39 -4.80 -2.94 -2.02 -1.13 0.62 2000.00 1 manzai[15] 0.44 0.02 1.06 -1.66 -0.27 0.44 1.17 2.54 2000.00 1 manzai[16] -3.56 0.04 1.64 -6.94 -4.62 -3.55 -2.48 -0.41 2000.00 1 manzai[17] -1.76 0.04 1.69 -4.98 -2.85 -1.76 -0.60 1.43 2000.00 1 manzai[18] -2.25 0.04 1.66 -5.43 -3.38 -2.29 -1.15 1.10 2000.00 1 manzai[19] -0.81 0.04 1.63 -3.99 -1.89 -0.77 0.24 2.44 2000.00 1 manzai[20] -0.62 0.04 1.80 -4.11 -1.84 -0.62 0.61 2.83 2000.00 1 manzai[21] 3.67 0.04 1.69 0.35 2.56 3.71 4.81 6.95 2000.00 1 manzai[22] 0.05 0.02 1.11 -2.12 -0.69 0.05 0.77 2.28 2000.00 1 manzai[23] 0.53 0.03 1.14 -1.73 -0.26 0.54 1.31 2.75 2000.00 1 manzai[24] -2.06 0.03 1.31 -4.67 -2.94 -2.07 -1.20 0.53 2000.00 1 manzai[25] 0.35 0.03 1.34 -2.33 -0.53 0.39 1.27 2.90 2000.00 1 manzai[26] -1.79 0.03 1.27 -4.23 -2.61 -1.79 -0.94 0.70 2000.00 1 manzai[27] -1.92 0.04 1.63 -5.06 -3.02 -1.88 -0.85 1.26 2000.00 1 manzai[28] -1.87 0.03 1.25 -4.33 -2.75 -1.81 -1.05 0.54 2000.00 1 manzai[29] -0.28 0.04 1.63 -3.51 -1.39 -0.26 0.82 2.98 2000.00 1 manzai[30] 1.00 0.02 1.10 -1.16 0.25 0.98 1.72 3.10 2000.00 1 manzai[31] -1.37 0.04 1.64 -4.64 -2.49 -1.36 -0.25 1.79 2000.00 1 manzai[32] -0.10 0.02 1.10 -2.21 -0.83 -0.09 0.66 2.07 2000.00 1 manzai[33] 1.21 0.03 1.53 -1.75 0.19 1.23 2.19 4.21 2000.00 1 manzai[34] 1.05 0.04 1.65 -2.18 0.01 1.07 2.10 4.28 2000.00 1 manzai[35] 0.89 0.02 1.05 -1.21 0.18 0.90 1.63 2.90 2000.00 1 manzai[36] -1.25 0.02 0.98 -3.07 -1.91 -1.27 -0.59 0.68 2000.00 1 manzai[37] 2.02 0.03 1.32 -0.54 1.12 2.03 2.89 4.63 2000.00 1 manzai[38] -2.62 0.03 1.28 -5.08 -3.51 -2.62 -1.73 -0.14 2000.00 1 manzai[39] 3.94 0.03 1.26 1.48 3.07 3.97 4.76 6.34 2000.00 1 manzai[40] 0.20 0.04 1.64 -3.06 -0.90 0.17 1.32 3.41 2000.00 1 manzai[41] 6.05 0.02 1.05 4.07 5.34 6.06 6.72 8.19 2000.00 1 manzai[42] 5.42 0.04 1.77 2.11 4.21 5.38 6.58 9.01 2000.00 1 manzai[43] 6.93 0.03 1.34 4.38 6.00 6.94 7.84 9.59 2000.00 1 manzai[44] -3.08 0.04 1.67 -6.42 -4.17 -3.03 -1.92 0.17 2000.00 1 manzai[45] 1.58 0.04 1.65 -1.63 0.42 1.55 2.76 4.74 2000.00 1 manzai[46] -1.40 0.03 1.53 -4.52 -2.42 -1.35 -0.32 1.51 2000.00 1 manzai[47] -1.71 0.03 1.26 -4.17 -2.55 -1.68 -0.86 0.74 2000.00 1 manzai[48] -1.00 0.04 1.67 -4.34 -2.12 -1.01 0.10 2.24 2000.00 1 manzai[49] -0.45 0.04 1.65 -3.59 -1.60 -0.50 0.70 2.79 2000.00 1 manzai[50] 1.30 0.04 1.64 -1.88 0.17 1.29 2.46 4.51 2000.00 1 manzai[51] 1.02 0.03 1.12 -1.14 0.24 1.01 1.78 3.16 2000.00 1 manzai[52] 3.01 0.02 0.74 1.56 2.52 3.00 3.52 4.42 2000.00 1 manzai[53] -3.71 0.02 0.98 -5.56 -4.38 -3.71 -3.05 -1.75 2000.00 1 manzai[54] -2.31 0.04 1.80 -5.77 -3.56 -2.26 -1.12 1.17 2000.00 1 manzai[55] 7.88 0.04 1.77 4.46 6.68 7.87 9.10 11.32 2000.00 1 manzai[56] -3.02 0.03 1.26 -5.48 -3.87 -3.02 -2.15 -0.50 2000.00 1 manzai[57] -2.46 0.02 1.08 -4.57 -3.22 -2.47 -1.74 -0.33 2000.00 1 manzai[58] -1.85 0.03 1.54 -4.81 -2.91 -1.85 -0.83 1.19 2000.00 1 manzai[59] 1.86 0.04 1.60 -1.09 0.76 1.87 2.96 4.96 2000.00 1 manzai[60] -4.02 0.04 1.67 -7.28 -5.17 -4.04 -2.83 -0.84 2000.00 1 manzai[61] 1.22 0.03 1.12 -0.99 0.44 1.23 1.93 3.42 2000.00 1 manzai[62] 1.36 0.02 0.91 -0.36 0.75 1.35 1.97 3.16 2000.00 1
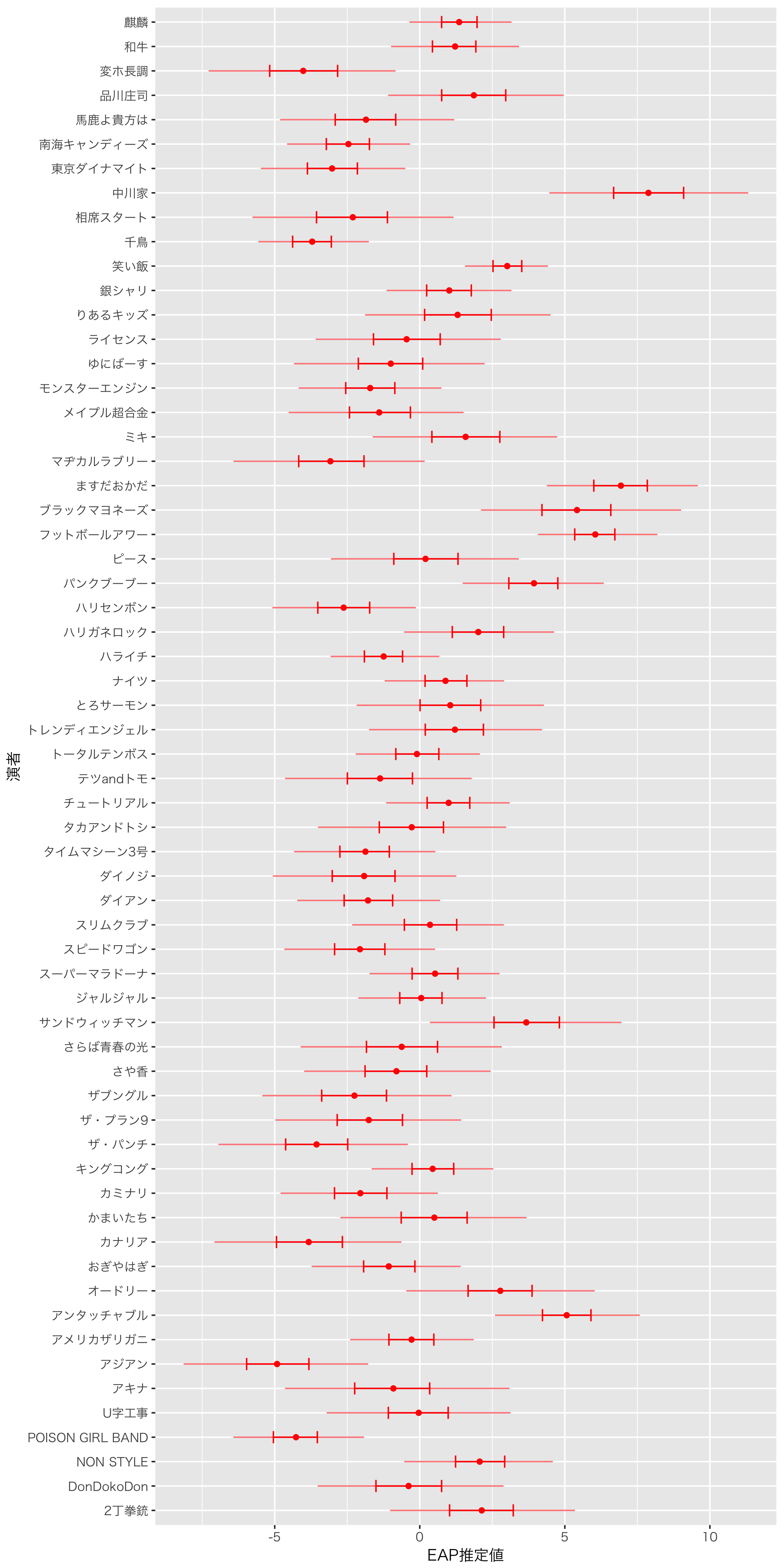
清水先生同様に小杉先生からコードをいただきまして,可視化しました。すると以下のようになります。
これをみると,中川家の漫才力がもっとも高いとわかります。推定の幅が広めですが。。
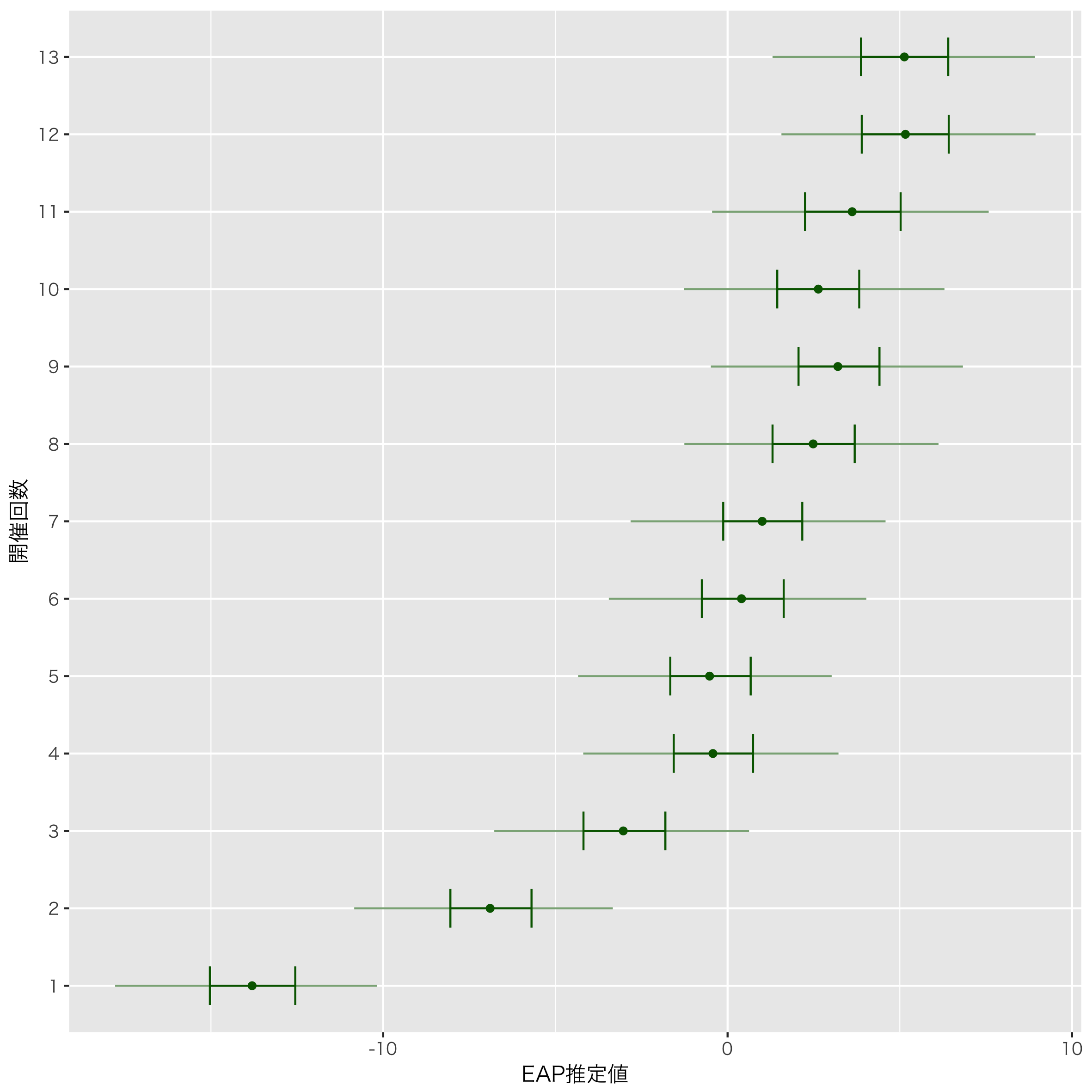
次に,年代による変量効果の推定です。
やはり初期のM-1は今と比べると採点が厳しかったようです。ここ数回は安定しているようですが,全体的には上昇傾向があるようにみえます。
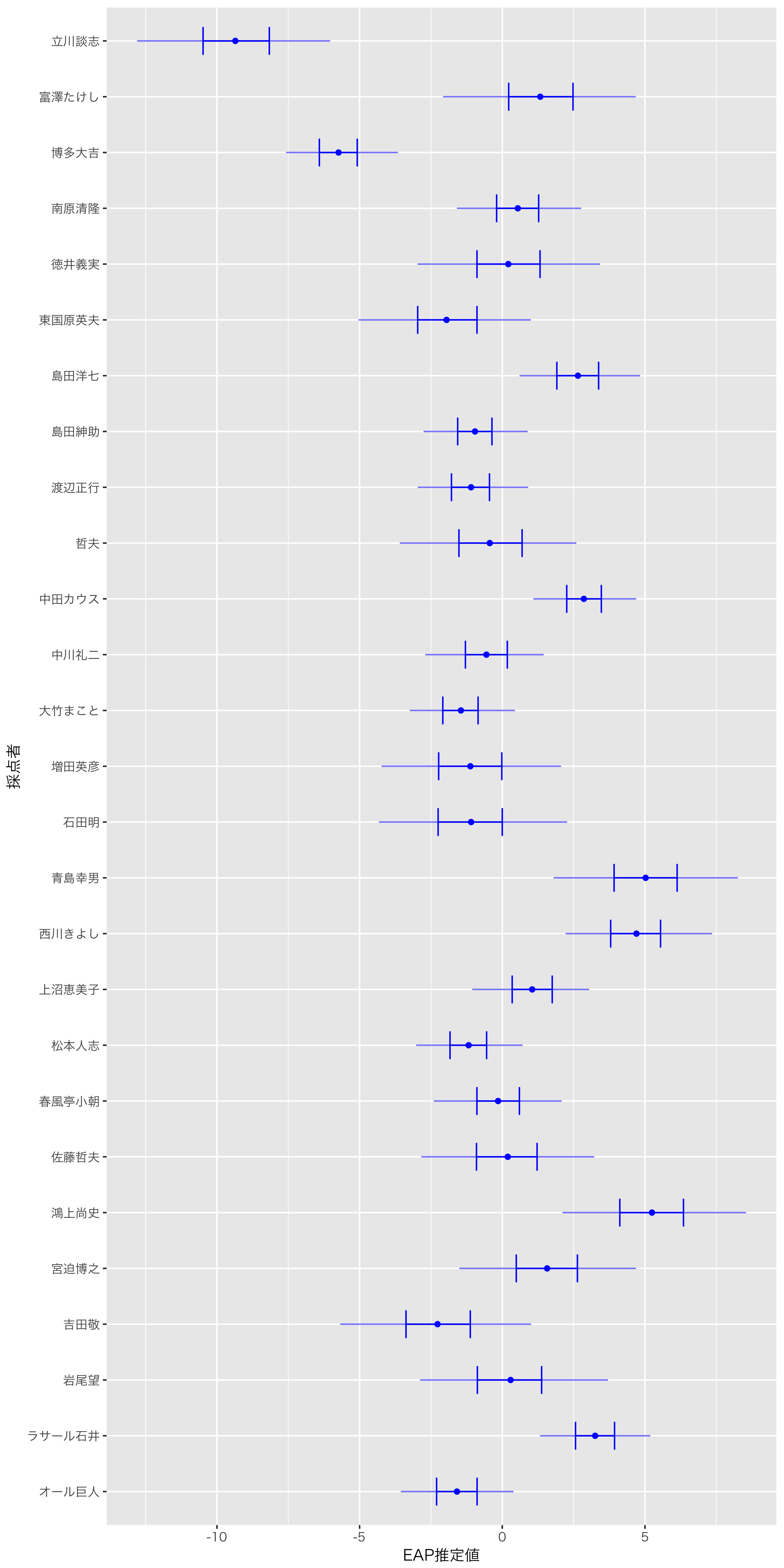
採点の甘さについても可視化してみます。
厳しいのは立川談志で清水先生の結果と変わりませんが,甘めな採点者が少し変わっています。鴻上尚史,西川きよし,青島幸男の採点が甘めであることがわかります。
ついでに,漫才力の平均得点と標準偏差,採点の甘さの標準偏差,年代の標準偏差を以下に示します。漫才力の平均得点は清水先生のモデルとほとんど変わりませんね。やはり年代の標準偏差は大きかったです。
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 86.95 0.11 1.85 83.31 85.72 86.92 88.14 90.70 294.48 1
sig_manzai 3.12 0.01 0.35 2.48 2.88 3.10 3.34 3.86 2000.00 1
sig_saiten 3.42 0.01 0.60 2.47 3.00 3.36 3.78 4.78 2000.00 1
sig_year 5.68 0.03 1.28 3.80 4.77 5.44 6.39 8.69 2000.00 1
結論
小杉先生のモデルではブラックマヨネーズ,清水先生のモデルではパンクブーブーが最強とのことでしたが,私のモデルでは中川家が最強ということになりました。ただし,やはり信用区間が広いので,ダントツでというわけではなさそうです。
私のモデルで中川家が最強となったのは,初期のころのM-1の採点の厳しさをモデルに入れ込んだためだと考えられます。第3回までの優勝者であるますだおかだやフットボールアワーが上位にきていることからもそういったことが予測されます。年代の補正が強すぎない?と思わなくもないのですが。。
この記事は3番煎じなので,本当はもっと凝ったモデルを考えてみようと思ったのですが,安直なモデル変更しかしていません。ですが,「最強のM-1漫才師は誰だ」シリーズへのチャレンジとしては面白い結果が出せたのではないでしょうか。
複数回出場している芸人の漫才力をどのように推定するか,決勝の最終得票数をどのように考慮するかなど,考えていくときっともっと面白いモデルが作れると思います。そして有意差のような差を示したわけではありませんが,モデルを少し変えるだけでもこうした順位が変わってしまうのは面白いですね。社会科学の再現性の話なんかを連想してしまいます。そもそもこういった賞レースには再現性なんてなさそうですが。そして,それでも予測できるモデルを考えたりしていると楽しいそうですね。
うまいこといって落とせませんが,Stanを使ったM-1記事お待ちしております。私もこういった分析を行い,記事を書くことになるとは,思ってもみませんでした。なんとなくのノリです。たぶんそんなもんでよいのです。
明日のM-1モデラーはあなたかもしれない!