2015年7月27日に比治山短期大学で開催された魁!!ベイズ塾でポワソン分布についての発表をしてきました。発表スライドはこんな感じです。
ベイズ塾での議論をふまえてポワソン分布について簡単にまとめ直してみようと思います。
ポワソン分布は2項分布の試行数(n)と成功確率(θ)の積で表現される値λを一定の値に保ち,そのλが与えられたときに確率変数Xが従う確率関数です。λは一定に保たれるので,試行数を無限大にしていくと成功確率は0に向かって極限していくことになります。具体的には,
f (x|λ) = e^-λ*λ^x / x!, 0 < x < ∞, xは整数
として定義されます。
これだけだとなんだかイメージしづらいので,ポワソン分布を適用できる具体例をみていきます。豊田先生の「基礎からのベイズ統計学」では,単位時間あたりの流れ星の数,交通事故数や綴りを間違える回数や,単位面積あたりのレストランの件数や爆弾命中数など多くの現象に適用できると書かれています。要は,回数や件数みたいに整数で数えられる現象で,比較的レアな現象であれば適用できるものと思われます。
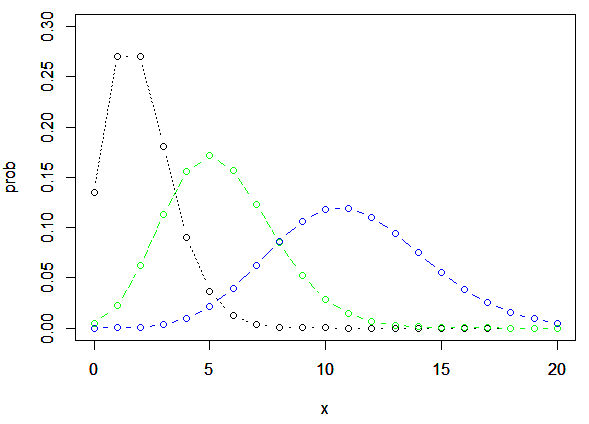
ポワソン分布はλのみによって分布の形が決定されるので,どんな分布なのかを考えるときに,λの大きさが重要になってきます。ということで,λを変えてポワソン分布の形をみてみます。
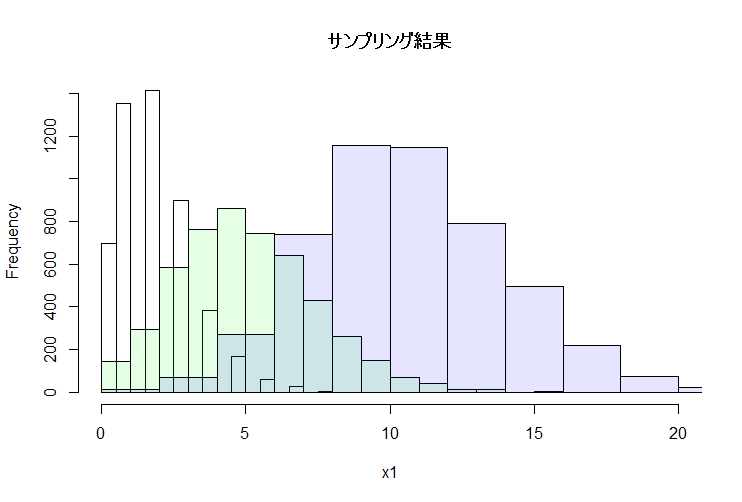
せっかくなのでrstanを使って,ポワソン分布に従うデータを生成し,それが上記のグラフのような形になるのか試してみます。下のコードで走らせているのは,上のグラフと同じようにλ=2, 5.5, 11.1のポワソン分布に従うデータをそれぞれ10000個ほど生成してます。rstanではバーンアウト区間がデフォルトだと半分に設定されているので,結果的にグラフ作成に使用しているのはそれぞれ5000個のデータになります。
rstanのstancodeの中身で,parameterブロックとmodelブロックは使用していないので関係ないのかと思いますが,これがないとうまく走りませんでした。。なぜなんだぜ。。
グラフをみてもらうと,最初に示したグラフと同じようなヒストグラムができあがっているのがわかると思います。
ちなみに,ポワソン分布のλは平均(期待値)や分散と等しくなる(λ = 平均 = 分散)という性質を持っています。なので,λを求めてるときは,平均値を求めてやればよいわけです。非常に簡単にλは求められますが,この「平均と分散が等しくなる」という仮定はなかなか厳しいもので,適合度を下げがち,ということが当日の議論では出てきました。また,その議論の中で,ポワソン分布は,λという1つのパラメタによって分布が定まってしまうため,個人差とかを検討しにくいねって話が出てきたりもしました。
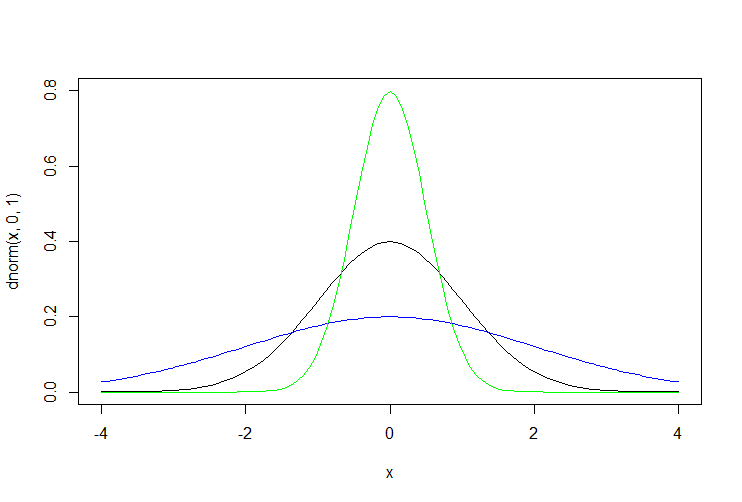
どういうことかというと,例えば正規分布だと,平均と分散という2つのパラメタによって分布の形が決まります。具体的には,平均を固定しても分散を自由に変動させることで,分布の形は変えられるます。ちなみに正規分布で平均固定して分散をを動かすと下の図ような分布になります。
だけど,ポワソン分布の場合,分散も平均と等しいという仮定されているので,正規分布みたいな表現ができないわけですね。「平均=分散」という仮定のおかけで,簡単にλは求められますが,データにフィットしないことも出てきやすくなってしまうわけです。これが緑本とかで指摘される過分散の問題だろうかとか思ったりしてます。
個人差が常に一定ではない教育心理学とか発達心理学の領域だと,こうした過分散とかの問題にぶち当たって,そのままだと適用に限界があるのかもしれないなーと。てなことで,データの生成メカニズムがポワソン分布なんだけど個人差を考慮したいって場合は,自然と階層ベイズって流れになりそうだぁと思ったりしてます。
ポワソン分布のハイパーパラメタを設定して階層ベイズにする場合は,ガンマ分布とか負の二項分布とかが共役関係にあるっぽいけど,どんな形状パラメタと尺度パラメタを組んだらよいかは,まだよくわかってないです。まだまだ勉強が必要なようです。
今回のベイズ塾のテーマは「分布感をつかむ」という謎テーマだったわけですが,個人的には得るもの多く,非常に有意義な時間が過ごせました。