この記事は、Stan Advent Calendar 2017の10日目のエントリーです。
昨年のアドカレにて,一般化極値分布の実装に関する記事を紹介したのですが,その際,時系列データを使ったにも関わらず状態空間モデルを使っていなかったので,使ってみましょうという趣旨になります。いろいろとやってみようと思ったのですが,まだまだ試行錯誤の段階で中途半端なところが多々ありますが,進捗報告として公開します。
以下の概要としては,
- 1階差分の状態空間モデル(正規分布ver.)
- 1階差分の状態空間モデル(一般化極値分布ver.)
- 2階差分の状態空間モデル(一般化極値分布ver.)
- 推定結果のプロットとWAICで比較
- 一般化極値分布で推定した場合のMCMC収束に関する問題点
なお,使ったデータは昨年の記事と同様に高松市の1時間あたりの最大降水量のデータ76年分です。
状態空間モデルについては,今年のアドカレでも何回もでてきていますし,ググればそれこそ様々な良記事がありますので,そちらを参考にしてみてください。いくつかお世話になったWebサイトや本を列挙しておきます。
- 二階差分の状態空間モデル,それより俺はいつからデブキャラになったんだ
- Stanで体重の推移をみつめてみた(状態空間モデル)
- 【読書会資料】『StanとRでベイズ統計モデリング』Chapter12:時間や空間を扱うモデル
- StanとRでベイズ統計モデリング
1階差分の状態空間モデル(正規分布ver.)
まずは練習がてら1階差分の状態空間モデルをよくみる正規分布にあてはめてやってみましょう。Stanコードはこんな感じです。
data {
int N;
vector[N] Y;
}
parameters {
real muZero; // 左端
vector[N] mu; // 確率的レベル
real<lower=0> sdV; // 観測誤差の大きさ
real<lower=0> sdY; // 過程誤差の大きさ
}
model {
// 状態方程式の部分
// 左端から初年度の状態を推定する
mu[1] ~ normal (muZero, sdY);
// 観測方程式の部分
for (i in 1:N) {
Y[i] ~ normal (mu[i], sdV);
}
// 状態の推移
for(i in 2:N) {
mu[i] ~ normal (mu[i-1], sdY);
}
sdV ~ cauchy (0, 5);
sdY ~ cauchy (0, 5);
}
generated quantities{
real log_lik[N];
for(i in 1:N){
log_lik[i] = normal_lpdf(Y[i]| mu, sdV);
}
}
推定結果は以下のような感じになりました。うん,収束してますね。31行目〜36行目はWAICを算出するために対数尤度を計算しています。
> print (fit03)
Inference for Stan model: rain_stan.
2 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=10000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero 29.40 0.14 3.21 21.73 27.84 29.84 31.37 34.75 527 1.00
mu[1] 29.39 0.14 3.10 22.06 27.84 29.81 31.34 34.58 492 1.01
mu[2] 29.46 0.13 2.95 22.64 27.91 29.83 31.30 34.52 503 1.01
mu[3] 29.61 0.11 2.78 23.34 28.07 29.92 31.36 34.59 663 1.00
mu[4] 29.77 0.09 2.64 23.87 28.31 30.01 31.39 34.55 842 1.00
mu[5] 29.92 0.07 2.53 24.38 28.48 30.11 31.50 34.63 1317 1.00
mu[6] 30.04 0.06 2.46 24.80 28.63 30.20 31.58 34.68 1592 1.00
<中略>
mu[74] 30.68 0.04 2.63 25.09 29.10 30.78 32.32 35.75 3549 1.00
mu[75] 30.69 0.04 2.69 24.99 29.08 30.83 32.33 36.03 3827 1.00
mu[76] 30.72 0.04 2.81 24.93 29.06 30.81 32.41 36.15 4038 1.00
sdV 11.39 0.02 0.97 9.74 10.71 11.33 12.02 13.43 2244 1.00
sdY 0.70 0.06 0.56 0.17 0.32 0.54 0.91 2.24 81 1.04
1階差分の状態空間モデル(一般化極値分布ver.)
先ほどを同じことを一般化極値分布でやってみましょう。一般化極値分布の確率密度関数は,
\[
g(z) = ({1/\sigma}) t(z)^{\xi+1}\mathrm{e}^{-t(z)} \\
\]
\[
t(z) = \begin{cases}
(1 + \xi((z – mu)/\sigma))^{-1/\xi} & (ただし, \xi \not= 0) \\
\mathrm{e}^{-(z-\mu)/\sigma} & (ただし, \xi = 0)
\end{cases}
\]
と表現できるようですので,Stanコードは以下のようにしています。
functions {
real gevmxt_lpdf(real y , real mu, real sigma, real xi){
real z;
real t;
z = 1 + (y - mu) * xi / sigma;
t = z ^(-1 / xi);
return log((( 1 / sigma)* t^( 1 + xi )* exp(-t)));
}
}
data {
int N;
vector[N] Y;
int<lower=0> predN;
}
parameters {
real muZero; // 左端
vector[N] mu; // 確率的レベル
vector<lower=0>[predN] pred_Y; //予測は欠測値として扱うパラメータ
real<lower=0, upper=30> siV; // sigma観測誤差の大きさ
real<lower=0, upper=30> siY; // sigma過程誤差の大きさ
real<lower=-0.5, upper=0.5> xiV; // xi観測誤差の大きさ
real<lower=-0.5, upper=0.5> xiY; // xi過程誤差の大きさ
}
model {
// 状態方程式の部分
// 左端から初年度の状態を推定する
mu[1] ~ gevmxt (muZero, siY, xiY);
// 観測方程式の部分
{
int npred;
npred = 0;
for(i in 1:N) {
if(Y[i]!=9999){
Y[i] ~ gevmxt (mu[i], siV, xiV);
}else{
npred = npred+1;
pred_Y[npred] ~ gevmxt (mu[i],siV, xiV);
}
}
}
// 状態の推移
for(i in 2:N) {
mu[i] ~ gevmxt (mu[i-1], siY, xiY);
}
siV ~ cauchy (0, 5);
siY ~ cauchy (0, 5);
}
generated quantities{
real log_lik[N];
for(i in 1:N){
log_lik[i] = gevmxt_lpdf(Y[i]| mu[i], siV, xiV);
}
}
このStanコードを使って推定してみた結果がこちら。収束はしているように思えます。iterationやchainは正規分布のときよりもちょこっと増やしています。ちょっと気になるのはn_effが少ないことと,simgaの状態方程式と観測方程式の値が大きく違うこと,そしてxiの状態方程式と観測方程式の値で正負が異なることでしょうか。これ大丈夫かな。。要検証です。
> print (fit01)
Inference for Stan model: rain_gev01.
4 chains, each with iter=15000; warmup=5000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero 22.62 0.13 2.41 17.16 21.28 22.87 24.21 26.75 356 1.01
mu[1] 22.72 0.12 2.33 17.51 21.39 22.94 24.26 26.76 357 1.02
mu[2] 22.84 0.12 2.23 17.88 21.55 23.04 24.32 26.78 371 1.02
mu[3] 22.98 0.11 2.14 18.30 21.72 23.15 24.40 26.82 402 1.01
mu[4] 23.11 0.10 2.06 18.67 21.88 23.26 24.49 26.87 425 1.01
mu[5] 23.23 0.10 2.00 18.99 22.02 23.36 24.57 26.92 439 1.01
<中略>
mu[72] 27.85 0.07 1.71 24.71 26.67 27.84 28.97 31.31 540 1.00
mu[73] 27.96 0.08 1.74 24.77 26.75 27.94 29.10 31.55 522 1.00
mu[74] 28.06 0.08 1.79 24.83 26.80 28.02 29.19 31.77 514 1.00
mu[75] 28.16 0.08 1.84 24.88 26.87 28.12 29.30 32.05 499 1.00
mu[76] 28.28 0.09 1.91 24.92 26.95 28.20 29.43 32.34 485 1.00
siV 9.01 0.02 0.88 7.44 8.39 8.97 9.57 10.91 1725 1.00
siY 0.28 0.02 0.29 0.03 0.10 0.19 0.33 1.13 203 1.02
xiV 0.02 0.00 0.09 -0.13 -0.04 0.01 0.08 0.21 1388 1.01
xiY -0.18 0.01 0.25 -0.49 -0.38 -0.24 -0.02 0.42 310 1.01
2階差分の状態空間モデル
アヒル本読書会の第6回Osaka.Stanに参加した際に聞いた@masashikomori先生の発表や@kosugitti先生のStanアドカレで取り上げられていますが,変化を推定しようとすると1階差分のモデルよりも2階差分のモデルのほうが良いらしいです。もしくは2階差分までとらないが,変化分を予測するローカル線形トレンドモデルなんかがよいとのことでした。
ローカル線形トレンドモデルの変化分をモデルに組み込むというのがいまいちわかっていないため,今回は2階差分の状態空間モデルを試してみようと思います。Stanコードは以下の通りです。
functions{
real gevmxt_lpdf(real y , real mu, real sigma, real xi){
real z;
real t;
z = 1 + (y - mu) * xi / sigma;
t = z ^(-1 / xi);
return log((( 1 / sigma)* t^( 1 + xi )* exp(-t)));
}
real gevmxt_lccdf(real y , real mu, real sigma, real xi){
real z;
real t;
z = 1 + (y - mu) * xi / sigma;
t = z ^(-1 / xi);
return log(1-exp(-t));
}
}
data{
int N;
vector[N] Y;
}
parameters{
real muZero; // 左端
vector[N] mu; // 確率的レベル
real<lower=0, upper=20> siV; // sigma観測誤差の大きさ
real<lower=0, upper=20> siY; // sigma過程誤差の大きさ
real<lower=-0.5, upper=0.5> xiV; // xi観測誤差の大きさ
real<lower=-0.5, upper=0.5> xiY; // xi過程誤差の大きさ
}
model{
// 状態方程式の部分
// 左端から初年度の状態を推定する
mu[1] ~ gevmxt (muZero, siY, xiY);
// 観測方程式の部分
for (i in 1:N) {
Y[i] ~ gevmxt (mu[i], siV, xiV);
}
// 状態の推移
for(i in 3:N){
mu[i] ~ gevmxt (2*mu[i-1] - mu[i-2], siY, xiY);
}
siV ~ cauchy (0, 5);
siY ~ cauchy (0, 5);
// xiV ~ uniform(-0.5, 0.5);
// xiY ~ uniform(-0.5, 0.5);
}
generated quantities{
real log_lik[N];
for(i in 1:N){
log_lik[i] = gevmxt_lpdf(Y[i]| mu[i], siV, xiV);
}
}
推定結果をみるとうまく収束してくれていたようです。でもこれ実はxiの事前分布を一様分布にすると収束しません。このあたりの話は最後に触れようと思います。
> print(fit)
Inference for Stan model: rain_stan.
2 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=10000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
muZero 29.40 0.14 3.21 21.73 27.84 29.84 31.37 34.75 527 1.00
mu[1] 29.39 0.14 3.10 22.06 27.84 29.81 31.34 34.58 492 1.01
mu[2] 29.46 0.13 2.95 22.64 27.91 29.83 31.30 34.52 503 1.01
mu[3] 29.61 0.11 2.78 23.34 28.07 29.92 31.36 34.59 663 1.00
mu[4] 29.77 0.09 2.64 23.87 28.31 30.01 31.39 34.55 842 1.00
mu[5] 29.92 0.07 2.53 24.38 28.48 30.11 31.50 34.63 1317 1.00
<中略>
mu[73] 30.70 0.04 2.56 25.35 29.16 30.77 32.28 35.68 3508 1.00
mu[74] 30.68 0.04 2.63 25.09 29.10 30.78 32.32 35.75 3549 1.00
mu[75] 30.69 0.04 2.69 24.99 29.08 30.83 32.33 36.03 3827 1.00
mu[76] 30.72 0.04 2.81 24.93 29.06 30.81 32.41 36.15 4038 1.00
sdV 11.39 0.02 0.97 9.74 10.71 11.33 12.02 13.43 2244 1.00
sdY 0.70 0.06 0.56 0.17 0.32 0.54 0.91 2.24 81 1.04
ついでに正規分布を用いた2階差分の状態空間モデルもやってみましたが,ところどころmuやsigmaやxiの値が収束していません
正規分布と一般化極値分布の比較
状態空間モデルの中で正規分布を用いた場合と一般化極値分布を用いた場合の推定結果を比較してみましょう。並べるとこんな感じになります(左上:ローデータ,左下:正規分布,右上:1階差分のGEV, 右下:2階差分のGEV)。
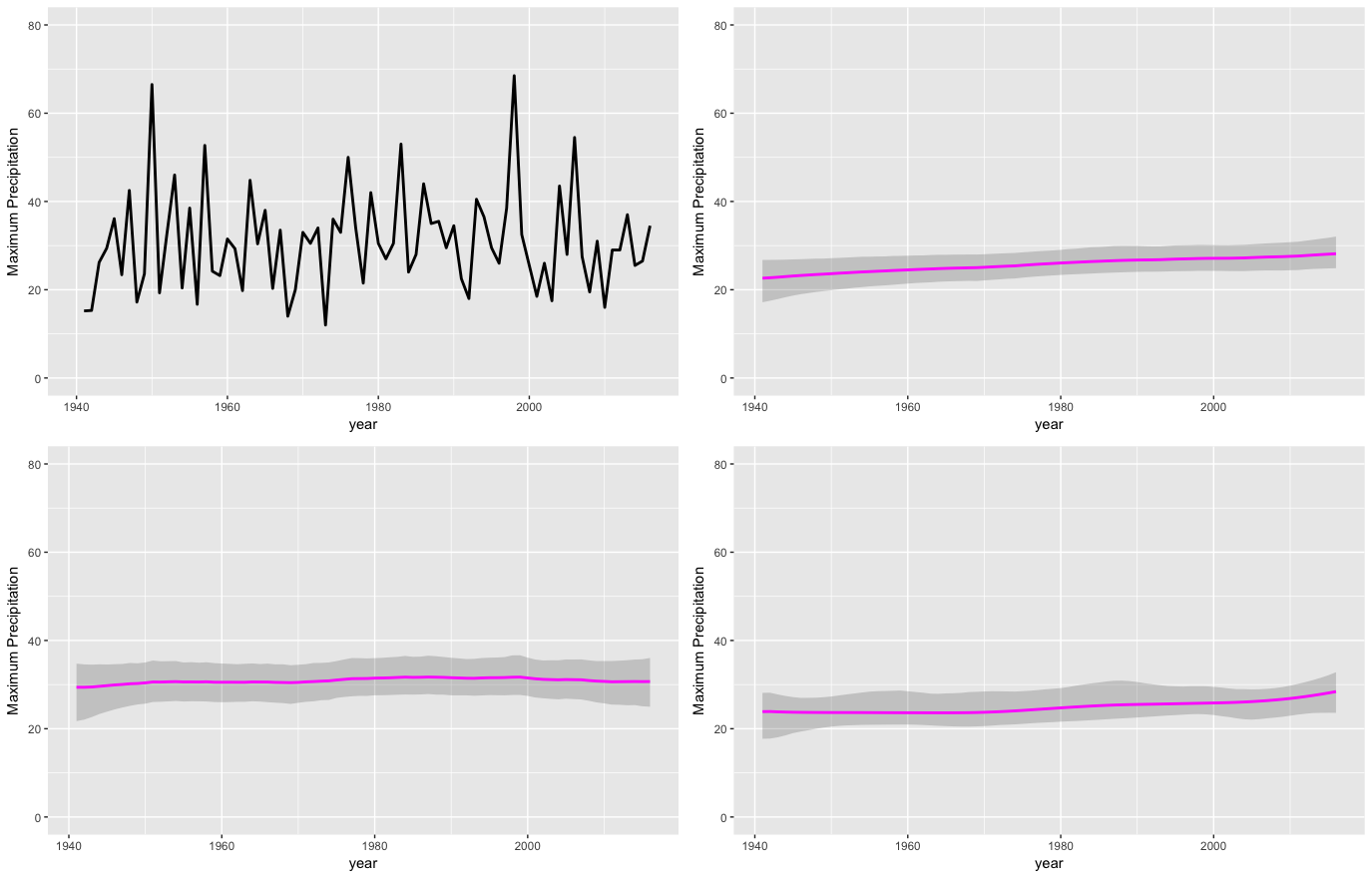
状態空間モデルを用いたmuの推定値の推移について正規分布と一般極値分布で比較した図。左上がローデータのプロット,左下が正規分布を用いた1階差分の状態空間モデル,右上が一般化極値分布を用いた1階差分の状態空間モデル,右下が一般化極値分布を用いた2階差分の状態空間モデル
正規分布で推定した場合には,ほとんど上昇傾向はないように思えますが,一般化極値分布を使うとうっすらと上昇傾向があるように見えます。あとは灰色で塗りつぶしてある95%信用区間が一般化極値分布をつかったほうが狭くなっているように感じます。2階差分モデルになると区間推定した部分もなめらかな感じになり面白いです。
データ生成メカニズム的には一般化極値分布のほうが適切だと思うのですが,どちらのモデルのほうがよいかをWAICで比較してみます。今回,WAICの算出にはloo packageの力を借りてます。コードは以下のようなものを実施しています。
library(loo) # 正規分布(予測なし)の場合 log_lik1 <- extract_log_lik(fit) waic1 <- waic(log_lik1) print(waic1 , digits = 3)
| 分布 | WAIC |
| 正規分布 | 74035.1796 |
| 一般化極値分布(1階差) | 577.3523 |
| 一般化極値分布(2階差) | 580.6330 |
比べると圧倒的ですね。正規分布の場合のWAICが74035に対して,一般化極値分布の場合のWAICは577, 580でした。一般化極値分布のほうが良さそうです。そして2階差分のモデルまでくんではみましたが,適合度的には1階差のほうがよいみたいです。・・・でもそれじゃ予測にあまり役立たなくない?
ちなみに10年後の最大降水量まで予測するモデルも試してみたのですが,2階差分モデルはうまく収束しなくて,うーんて感じになってます。
一般化極値分布で推定した場合のMCMC収束に関する問題点
問題点
- 3パラメタのため,収束しにくい
- xiの振る舞いがそもそもわかりにくい
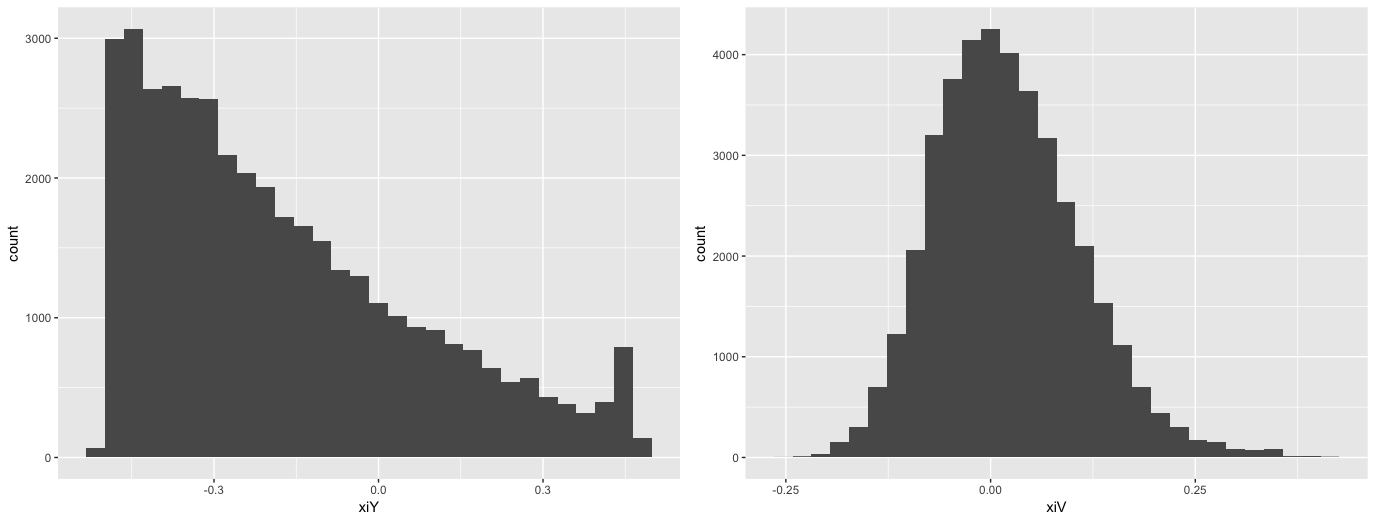
今回の推定では,最大値を使った分析では一般化極値分布を使うと良さそうだという結論がえられたと思います。ただ,xiに関して状態方程式と観測方程式でかなり推定値が異なることが気になったので,1階差分のモデルの結果から状態方程式と観測方程式のxiの分布を確認してみました。すると以下のようになります。
左が観測方程式の,右が状態方程式の中のxiの分布です。潜在変数と観測変数でこんな違うのはありですか?ちょっとまずくないかと思ったりするわけです。これちなみに一様分布を使うと観測方程式の中のxiは真っ平らになります。今回はxiの範囲を-0.5:0.5の間に指定してしまっていたので,それが問題なのかもしれません。
よくよく考えたら私は一般化極値分布のxiというパラメタがどのような振る舞いをするのかよく知りません。一般化極値分布について,理想的なデータをつくり,それぞれのパラメタがどのような振る舞いをするのか,丁寧に確認していく必要がありそうです。
さしあたって,今後の私の課題としては,
- 一般化極値分布の各パラメタの挙動について理解すること
- 未来の予測を含むモデルで一般化極値分布を使用すること
- ローカル線系トレンドモデルの導入
あたりになるでしょうか。